题目内容
如图，将等腰直角△ABC沿斜边BC方向平移得到△A1B1C1．若AB=3，若△ABC与△A1B1C1重叠部分面积为2，则BB1的长为 ．
【答案】分析：重叠部分为等腰直角三角形，设B1C=2x，则B1C边上的高为x，根据重叠部分的面积列方程求x，再求BB1．
解答：解：设B1C=2x，
根据等腰三角形的性质可知，重叠部分为等腰直角三角形，
则B1C边上的高为x，
∴
×x×2x=2，解得x=
（舍去负值），
∴B1C=2
，
∵AB=AC=3，
∴BC=
=3
，
∴BB1=BC-B1C=
．
故答案为：
．
点评：本题考查了等腰直角三角形的性质，平移的性质．关键是判断重叠部分图形为等腰直角三角形，利用等腰直角三角形的性质求斜边长．
解答：解：设B1C=2x，
根据等腰三角形的性质可知，重叠部分为等腰直角三角形，
则B1C边上的高为x，
∴
×x×2x=2，解得x=（舍去负值），∴B1C=2
，∵AB=AC=3，
∴BC=
=3，∴BB1=BC-B1C=
．故答案为：
．点评：本题考查了等腰直角三角形的性质，平移的性质．关键是判断重叠部分图形为等腰直角三角形，利用等腰直角三角形的性质求斜边长．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
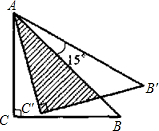如图，将等腰直角三角形ABC绕点A逆时针旋转15°后得到△AB′C′，若AC=1，则图中阴影部分的面积为（ ）A、
| ||||
B、
| ||||
C、
| ||||
D、3
|
如图，将等腰直角△ABC沿BC方向平移得到△A1B1C1．若BC=3
如图，将等腰直角三角形ABC绕点A逆时针旋转15°后得到△AB′C′，若AC=1，则图中阴影部分的面积为
如图，将等腰直角△ABC（∠ACB=90°，AC=BC）绕C点按逆时针方向旋转到△A'CB'的位置，若∠A'+∠A'CB=170°，则∠ACB'等于（ ）
如图，将等腰直角△ABC沿BC方向平移得到△A1B1C1，若BC=