Question

【题目】如图，在△ABC 中，∠ C=90°，AC=5，BC=12，D 是 BC 边的中点．

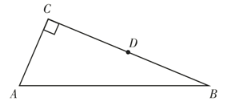
（1）尺规作图：过点 D 作 DE⊥AB 于点 E；(保留作图痕迹，不写做法)

（2）求 DE 的长

Answer 1

【答案】（1）见解析；（2）

【解析】

（1）以点D为圆心作一段弧交AB于两点，以这两点为圆心，分别作圆弧交于一点，将D与该点连接即可求作出E；

（2）由勾股定理可求出AB=13，又易证△ACB∽△DEB，从而可知，化简即可求出DE的长度．

解：（1）以点D为圆心作一段弧交AB于两点，以这两点为圆心，分别作圆弧交于一点，将D与该点连接即可求作出E，如图所示：

（2）∵点D为BC中点，

∴，

又∵在Rt△ACB中，∠C=90°，AC=5，BC=12，

∴AB=13，

又∵∠C=∠DEB=90°，∠B=∠B，

∴△ACB∽△DEB，

∴，

∴，即DE=.