题目内容
等腰三角形ABC中，∠A=120°，BC中点为D，过D作DE⊥AB于E，AE=4 cm，则AD等于
- A.8cm
- B.7cm
- C.6cm
- D.4cm
A
分析：根据等腰三角形的性质和直角三角形的性质求解．
解答：
解：∵等腰三角形ABC中，∠A=120°，BC中点为D，
∴∠BAD=∠CAD=60°，
∵DE⊥AB，AE=4cm，
∴AD=2AE=8cm．
故选A．
点评：此题考查学生对等腰三角形三线合一的掌握及直角三角形的性质的运用．
分析：根据等腰三角形的性质和直角三角形的性质求解．
解答：
解：∵等腰三角形ABC中，∠A=120°，BC中点为D，∴∠BAD=∠CAD=60°，
∵DE⊥AB，AE=4cm，
∴AD=2AE=8cm．
故选A．
点评：此题考查学生对等腰三角形三线合一的掌握及直角三角形的性质的运用．
练习册系列答案
相关题目
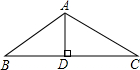如图所示，在等腰三角形ABC中，AB=AC=12cm，∠ABC=30°，那么底边上的高AD=
如图，等腰三角形ABC中，AB=AC，AD是底边BC上的中线，若AB=10，BC=12，则中线AD的长度为（ ）