题目内容
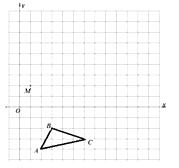
【题目】△ABC在平面直角坐标系中的位置如图所示.
(1)将△ABC向右平移6个单位,作出平移后的△A1B1C1,并写出△A1B1C1各顶点的坐标;
(2)在y轴上是否存在点M,使得CM+BM最小?若存在,求出点M坐标;若不存在,请说明理由.
【答案】(1)A1(6,4),B1(4,2),C1(5,1);(2)(0,![]() )
)
【解析】
(1)分别作出点A,B,C向右平移6个单位得到的对应点,再顺次连接即可得;
(2)作出点C关于y轴的对称点C′,连接C′B,与y轴的交点即为所求,再利用待定系数法求出直线C′B的解析式,求出与y轴的交点即可.
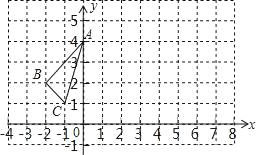
解:(1)如图所示,△A1B1C1即为所求,

由图知A1点的坐标为(6,4),B1点的坐标为(4,2),C1点的坐标为(5,1);
(2)点C(﹣1,1)关于y轴的对称点C′的坐标为(1,1),
设直线C′B的解析式为y=kx+b,
则![]()
解得: 
∴直线C′B的解析式为y=﹣![]() x+
x+![]() ,
,
当x=0时,y=![]() ,
,
∴点M的坐标为(0,![]() ).
).

练习册系列答案
相关题目