题目内容
已知△ABC≌△DEF，AB=2，AC=4，若△DEF的周长为偶数，则EF的取值为
- A.3
- B.4
- C.5
- D.3或4或5
B
分析：因为两个全等的三角形对应边相等，所以求EF的长就是求BC的长．
解答：4-2＜BC＜4+2
2＜BC＜6．
若周长为偶数，BC也要取偶数所以为4．
所以EF的长也是4．
故选B．
点评：本题考查全等三角形的性质，全等三角形的对应边相等，以及三角形的三边关系．
分析：因为两个全等的三角形对应边相等，所以求EF的长就是求BC的长．
解答：4-2＜BC＜4+2
2＜BC＜6．
若周长为偶数，BC也要取偶数所以为4．
所以EF的长也是4．
故选B．
点评：本题考查全等三角形的性质，全等三角形的对应边相等，以及三角形的三边关系．
练习册系列答案
全能测控一本好卷系列答案
相关题目
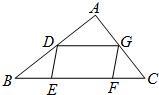8、△ABC与平行四边形DEFG如图放置，点D，G分别在边AB，AC上，点E，F在边BC上．已知BE=DE，CF=FG，则∠A的度数（ ）
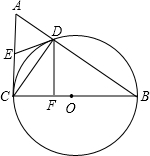（2012•郧县三模）如图，已知△ABC中，AB=10，BC=8，AC=6，以BC为直径作⊙O，交AB边于点D，过点D作DF⊥BC，垂足为F，E为AC中点，连接DE．
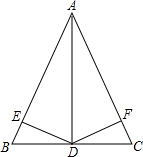如图，已知△ABC中，D是BC上一点，DE⊥AB，DF⊥AC，垂足分别为E、F．如果DE=DF，∠BAC=60°，AD=20cm，那么DE的长是