题目内容
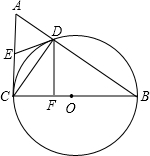（2012•郧县三模）如图，已知△ABC中，AB=10，BC=8，AC=6，以BC为直径作⊙O，交AB边于点D，过点D作DF⊥BC，垂足为F，E为AC中点，连接DE．（1）求证：DE是⊙O的切线；
（2）求DF的长；
（3）在BC上是否存在一点P，使DP+EP最小？若存在，求出点P的位置；若不存在，请说明理由．
分析：（1）连接DE，则可得ED=EA=EC，从而可得∠ECD=∠EDC，再由OC=OD，可得∠OCD=∠ODC，结合∠ECD+∠OCD=90°可证明OD⊥ED，继而可得出结论；
（2）根据△BCD∽△BAC，可得出BD的长度，然后根据△BDF∽△BAC，可求出DF的长度．
（3）延长DF交圆O于点H，连接ED'，则ED'与BC的交点即是点P的位置，然后求出CF，结合△ECP∽△D'FP可求出CP的长度．
（2）根据△BCD∽△BAC，可得出BD的长度，然后根据△BDF∽△BAC，可求出DF的长度．
（3）延长DF交圆O于点H，连接ED'，则ED'与BC的交点即是点P的位置，然后求出CF，结合△ECP∽△D'FP可求出CP的长度．
解答：解：（1）连接OD，
∵BC是直径，
∴∠CDB=90°，也可得出∠CDA=90°，
又∵点E是AC的中点，
∴ED=EC=EA，
∴∠ECD=∠EDC，
∵OD=OC，
∴∠OCD=∠ODC，
又∵∠ECD+∠OCD=90°，
∴∠EDC+∠ODC=90°，
∴OD⊥ED，
故DE是⊙O的切线．
（2）∵AB=10，BC=8，AC=6，
∴AC2+BC2=AB2，
∴∠BCA=90°，
∵∠B=∠B，∠BDC=∠BCA=90°，
∴△BCD∽△BAC，
∴
=
，即
=
，
解得：BD=
，
又∵∠B=∠B，∠BFD=∠BCA=90°，
∴△BDF∽△BAC，
∴
=
，即
=
，
解得：DF=
．
（3）
∵∠DCF=∠BAC，∠DFC=∠BDC=90°，
∴△BAC∽△DCF，
∴
=
，即
=
，
解得：CF=
，
∵∠BCA=∠CFD'=90°，∠EPC=∠D'PF，
∴△ECP∽△D'FP，
从而
=
，即
=
=
，
又∵CP+FP=CP=
，
∴CP=
．即点P的位置在距离C点右方
远处．
∵BC是直径，
∴∠CDB=90°，也可得出∠CDA=90°，
又∵点E是AC的中点，
∴ED=EC=EA，
∴∠ECD=∠EDC，
∵OD=OC，
∴∠OCD=∠ODC，
又∵∠ECD+∠OCD=90°，
∴∠EDC+∠ODC=90°，
∴OD⊥ED，
故DE是⊙O的切线．
（2）∵AB=10，BC=8，AC=6，
∴AC2+BC2=AB2，
∴∠BCA=90°，
∵∠B=∠B，∠BDC=∠BCA=90°，
∴△BCD∽△BAC，
∴
| BD |
| BC |
| BC |
| AB |
| BD |
| 8 |
| 8 |
| 10 |
解得：BD=
| 32 |
| 5 |
又∵∠B=∠B，∠BFD=∠BCA=90°，
∴△BDF∽△BAC，
∴
| BD |
| BA |
| DF |
| AC |
| BD |
| 10 |
| DF |
| 6 |
解得：DF=
| 96 |
| 25 |
（3）
∵∠DCF=∠BAC，∠DFC=∠BDC=90°，
∴△BAC∽△DCF，
∴
| CF |
| AC |
| DF |
| BC |
| CF |
| 6 |
| DF |
| 8 |
解得：CF=
| 72 |
| 25 |
∵∠BCA=∠CFD'=90°，∠EPC=∠D'PF，
∴△ECP∽△D'FP，
从而
| CP |
| PF |
| CE |
| FD′ |
| CP |
| PF |
| 3 | ||
|
| 25 |
| 32 |
又∵CP+FP=CP=
| 72 |
| 25 |
∴CP=
| 24 |
| 19 |
| 24 |
| 19 |
点评：本题属于圆的综合题，涉及了相似三角形的判定与性质、勾股定理的逆定理、轴对称求最短路径的问题，综合性较强，难度较大，解答本题的关键是熟练各个知识点的内容，将所学的知识融会贯通．
练习册系列答案
期末集结号系列答案
相关题目
（2012•郧县三模）如图，已知直线y=kx+b（k＞0）与抛物线y=x2交于A、B两点（A、B两点分别位于第二和第一象限），且A、B两点的纵坐标分别是1和9，则不等式x2-kx-b＞0的解集为（ ）
（2012•郧县三模）如图，⊙O的圆心在坐标原点，⊙O与x轴正半轴交于点B，延长OB至点A使AB=OB，过点A作⊙O的切线AC，切点为C，P为⊙O上一点（不在弧BC上），则cos∠BPC的值为（ ）