题目内容
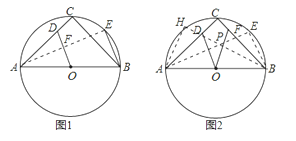
【题目】已知:⊙O为Rt△ABC的外接圆,点D在边AC上,AD=AO;
(1)如图1,若弦BE∥OD,求证:OD=BE;
(2)如图2,点F在边BC上,BF=BO,若OD=2![]() , OF=3,求⊙O的直径.
, OF=3,求⊙O的直径.

【答案】(1)证明见解析;(2)圆的直径为![]() .
.
【解析】试题分析:(1)连接AE交OD于点F,由AB为直径,利用直角所对的圆周角为直角得到AE与BE垂直,再由BE与OD平行,得到AE垂直于OD,再由AD=AO,利用三线合一得到AE为角平分线,且F为OD中点,利用中位线定理得到BE=2OF,等量代换即可得证;
(2)分别作弦BE∥OD,AH∥OF,连接AE,BH,AE与BH交于点P,由(1)得到E与H分别为弧BC与弧AC的中点,进而确定出∠HAE=∠HBE=45°,根据AB为直径,得到所对的圆周角为直角,确定出三角形APH与三角形BEP都为等腰直角三角形,由AP+PE求出AE的长,在直角三角形AEB中,利用勾股定理求出AB的长,即为圆的直径.
试题解析:解:(1)证明:连接AE交OD于点F.∵AB为直径,∴AE⊥BE,∵BE∥OD,∴AE⊥OD,∵AD=AO,∴AE平分∠CAB,∴OD=2OF,∵BE=2OF,∴BE=OD;
(2)分别作弦BE∥OD,AH∥OF,连接AE,BH,AE与BH交于点P,由(1)得:E为弧BC的中点,同理H为弧AC的中点,∴∠HAE=∠HBE=45°,∵AB为直径,∴∠H=∠E=90°,∴AP=![]() AH,PE=BE,∵点O为AB的中点,BE∥OD,∴EB=OD=
AH,PE=BE,∵点O为AB的中点,BE∥OD,∴EB=OD=![]() ,∴PE=BE=
,∴PE=BE=![]() ,同理AH=OF=3,∴AP=
,同理AH=OF=3,∴AP=![]() ,在Rt△ABE中,AE=
,在Rt△ABE中,AE=![]() ,BE=
,BE=![]() ,根据勾股定理得:AB=
,根据勾股定理得:AB=![]() ,则圆的直径为
,则圆的直径为![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目