��Ŀ����
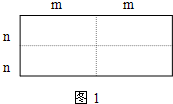
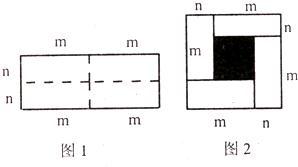
��ͼ1��һ����Ϊ2m����Ϊ2n�ij����Σ���ͼ�������ü������ֳ��Ŀ�С�����Σ�Ȼ��ͼ2����״ƴ��һ�������Σ�

��1������Ϊͼ2�е���Ӱ���ֵ������εı߳����ڶ���?

��2���������ֲ�ͬ�ķ�����ͼ14����Ӱ���ֵ������
����1��
����2��
��3���۲�ͼ2����д��������������ʽ֮��ĵ�����ϵ��
����ʽ����m+n��2����m��n��2��mn��
��4�����ݣ�3�����еĵ�����ϵ������������⣺��a+b=7��ab=5����a��b��2= ��
����1��
����2��
��3���۲�ͼ2����д��������������ʽ֮��ĵ�����ϵ��
����ʽ����m+n��2����m��n��2��mn��
��4�����ݣ�3�����еĵ�����ϵ������������⣺��a+b=7��ab=5����a��b��2= ��
�⣺��1��ͼ2�е���Ӱ���ֵ������εı߳����ڣ�m��n����
��2������һ����Ӱ���ֵ����=��m+n��2��2m2n��
����������Ӱ���ֵı߳�=m��n������Ӱ���ֵ����=��m��n��2��
��3����������ʽ֮��ĵ�����ϵ�ǣ���m+n��2=��m��n��2+4mn��
��4����a��b��2=��a+b��2��4ab=29��
��2������һ����Ӱ���ֵ����=��m+n��2��2m2n��
����������Ӱ���ֵı߳�=m��n������Ӱ���ֵ����=��m��n��2��
��3����������ʽ֮��ĵ�����ϵ�ǣ���m+n��2=��m��n��2+4mn��
��4����a��b��2=��a+b��2��4ab=29��

��ϰ��ϵ�д�
 �����������һ��һ��ϵ�д�
�����������һ��һ��ϵ�д� Ӧ������ҵ��ϵ�д�
Ӧ������ҵ��ϵ�д�
�����Ŀ

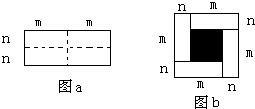 24����ͼa��һ����Ϊ2m����Ϊ2n�ij����Σ���ͼ�������ü������ȷֳ��Ŀ�С�����Σ�Ȼ��ͼb��״ƴ��һ�������Σ�
24����ͼa��һ����Ϊ2m����Ϊ2n�ij����Σ���ͼ�������ü������ȷֳ��Ŀ�С�����Σ�Ȼ��ͼb��״ƴ��һ�������Σ�
