题目内容
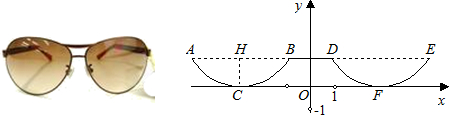
如图是一副眼镜镜片下半部分轮廓对应的两条抛物线关于y轴对称．AB∥x轴，AB=4cm，最低点C在x轴上，高CH=1cm，BD=2cm．则右轮廓线DFE的函数解析式为（ ）
A．
B．
C．
D．
【答案】分析：利用坐标系易得A、B、C三点的坐标，根据待定系数法就可以求出抛物线的解析式，再利用二次函数关于y轴对称的性质，即可得出答案．
解答：解：设左轮廓线ACB的抛物线解析式为y=ax2+bx+c（a≠0），
∵A（-5，1），B（-1，1），C（-3，0），
∴
，
解得：
；
∴左轮廓线ACB的抛物线解析式为：y=
x2+
x+
；
由左右两轮廓线关于y轴对称，y=
x2+
x+
=
（x+3）2，
∴右轮廓线DFE的函数解析式为：y=
（x-3）2，
故选：C．
点评：本题主要考查了待定系数法求抛物线的解析式，利用坐标系得出点的坐标，进而得出解析式是解题关键．
解答：解：设左轮廓线ACB的抛物线解析式为y=ax2+bx+c（a≠0），
∵A（-5，1），B（-1，1），C（-3，0），
∴
，解得：
；∴左轮廓线ACB的抛物线解析式为：y=
x2+x+；由左右两轮廓线关于y轴对称，y=
x2+x+=（x+3）2，∴右轮廓线DFE的函数解析式为：y=
（x-3）2，故选：C．
点评：本题主要考查了待定系数法求抛物线的解析式，利用坐标系得出点的坐标，进而得出解析式是解题关键．
练习册系列答案
相关题目
