题目内容
【题目】已知：如图，在△ABC中，M、N分别是边AB、AC的中点，D是边BC延长线上的一点，且CD= 
BC，联结CM、DN． 求证：四边形MCDN是平行四边形．
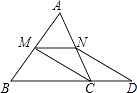
【答案】证明：∵点M、N分别是AB、AC的中点， ∴MN∥BC，且MN= 
BC．
即：MN∥CD．
又 CD= BC，
∴MN=CD．
∴四边形MCDN是平行四边形
【解析】根据三角形中位线的性质可得MN∥BC，且MN= 
BC，再由条件CD= BC可得MN=CD，进而可根据一组对边平行且相等的四边形是平行四边形得四边形MCDN是平行四边形．
【考点精析】解答此题的关键在于理解平行四边形的判定的相关知识，掌握两组对边分别平行的四边形是平行四边形：两组对边分别相等的四边形是平行四边形；一组对边平行且相等的四边形是平行四边形；两组对角分别相等的四边形是平行四边形；对角线互相平分的四边形是平行四边形．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
【题目】某班10名学生的校服尺寸与对应人数如表所示：
尺寸（cm） | 160 | 165 | 170 | 175 | 180 |
学生人数（人） | 1 | 3 | 2 | 2 | 2 |
则这10名学生校服尺寸的众数和中位数分别为（ ）
A.165cm，165cm
B.165cm，170cm
C.170cm，165cm
D.170cm，170cm