题目内容
【题目】探究活动:
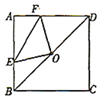
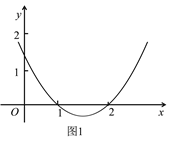
利用函数![]() 的图象(如图1)和性质,探究函数
的图象(如图1)和性质,探究函数![]() 的图象与性质.
的图象与性质.
下面是小东的探究过程,请补充完整:
(1)函数![]() 的自变量x的取值范围是___________;
的自变量x的取值范围是___________;
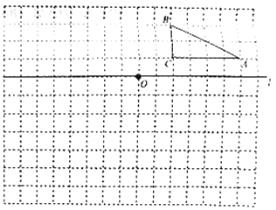
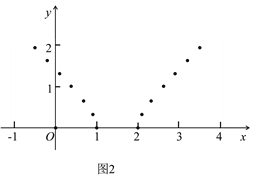
(2)如图2,小东列表描出了函数![]() 图象上部分点,请画出函数图象;
图象上部分点,请画出函数图象;
(3)解决问题:设方程![]() 的两根为
的两根为![]() 、
、![]() ,且
,且![]() ,方程
,方程
![]() 的两根为
的两根为![]() 、
、![]() ,且
,且![]() .若
.若![]() ,则
,则![]() 、
、![]() 、
、![]() 、
、![]() 的大小关系为_____________________(用“<”连接).
的大小关系为_____________________(用“<”连接).
【答案】(1)![]() 或
或![]() ;(2)见解析;(3)x1<x3<x4<x2
;(2)见解析;(3)x1<x3<x4<x2
【解析】(1)根据二次根式的性质,列出不等式,解之即可;
(2)由于x≤1或x≥2,所以函数图象应该是两条分支,根据对称性,补全另一分支即可;
(3)将方程的根转化为两函数图象交点的横坐标,作出函数图象,一目了然.
(1)∵(x-1)(x-2)≥0,
∴x≤1或x≥2;
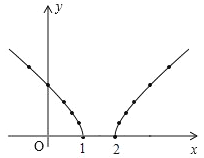
(2)根据自变量x的取值范围可知,当x≥2时也有对应的函数图象,
补全后的函数图象如图所示:
(3)方程![]() 等价于方程
等价于方程![]() ,
,
方程的两根x1、x2相当于函数y=![]() 与函数
与函数![]() 图象的两个交点的横坐标,
图象的两个交点的横坐标,
方程x2-3x+2=![]() x+b的两根为x3、x4,相当于函数y=x2-3x+2=(x-1)(x-2)与函数y=
x+b的两根为x3、x4,相当于函数y=x2-3x+2=(x-1)(x-2)与函数y=![]() x+b图象的两个交点的横坐标,
x+b图象的两个交点的横坐标,
又∵1<b<![]() ,
,
所以,在同一平面直角从标系中,画出函数图象,如图所示:
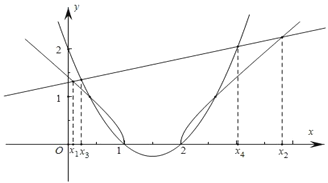
故x1<x3<x4<x2.

练习册系列答案
相关题目