Question

【题目】如图，在直角三角形ABC中，∠ABC＝90°.

(1)先作∠ACB的平分线；设它交AB边于点O，再以点O为圆心，OB为半径作⊙O(尺规作图，保留作图痕迹，不写作法)；

(2)证明：AC是所作⊙O的切线；

(3)若BC＝，∠A＝30°，求△AOC的面积．

Answer 1

【答案】（1）详见解析；（2）详见解析；（3）

【解析】

（1）根据角平分线的作法求出角平分线FC，进而得出⊙O；

（2）根据切线的判定定理求出EO=BO，即可得出答案；

（3）根据锐角三角函数的关系求出AC，EO的长，即可得出答案．

（1）解：如图所示：

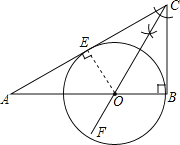
（2）证明：过点O作OE⊥AC于点E，

∵FC平分∠ACB，

∴OB=OE，

∴AC是所作⊙O的切线；

（3）解：∵∠A=30°，∠ABC=90°

∴∠ACO=∠OCB=∠ACB=30°，

∵BC=，

∴AC=2，BO=tan30°BC==1，

∴△AOC的面积为：×AC×OE=×2×1=．