题目内容
在平面直角坐标系中,O是坐标原点,A、B两点的坐标分别为(-1,0)、(0,3),以AB为边向右侧作正方形ABCD.求点C和点D的坐标.
考点:正方形的性质,坐标与图形性质
专题:
分析:由四边形AOCB是正方形可以得出AB=BC=CD=AD,∠ABC=∠BCD=∠DAB=∠CDA=90°,然后分别作CE⊥y轴于E,CF⊥x轴于F,DG⊥x轴于G,再根据△BEC≌△AOB≌△GDA得出EC=OB=AG=3,BE=AO=DG=1,进而得出OE=OB-BE=3-1=2,OG=AD-OA=3-1=2,就可以求出C、D的坐标.
解答: 解:CE⊥y轴于E,CF⊥x轴于F,DG⊥x轴于G.
解:CE⊥y轴于E,CF⊥x轴于F,DG⊥x轴于G.
∵四边形AOCB是正方形,
∴AB=BC=CD=AD,∠ABC=∠BCD=∠DAB=∠CDA=90°.
∵A、B两点的坐标分别为(-1,0)、(0,3),
∴AB=
=
∵∠ABO+∠EBC=∠ABO+∠BAO=∠BAO+∠DAG=∠DAG+∠ADG=90°,
∴∠EBC=∠BAO=∠ADG,
在△BEC和△AOB与△GDA中,
,
∴△BEC≌△AOB≌△GDA(AAS),
∴EC=OB=AG=3,BE=AO=DG=1,
∴OE=OB-BE=3-1=2,OG=AD-OA=3-1=2,
∴C(3,2),D(2,1).
 解:CE⊥y轴于E,CF⊥x轴于F,DG⊥x轴于G.
解:CE⊥y轴于E,CF⊥x轴于F,DG⊥x轴于G.∵四边形AOCB是正方形,
∴AB=BC=CD=AD,∠ABC=∠BCD=∠DAB=∠CDA=90°.
∵A、B两点的坐标分别为(-1,0)、(0,3),
∴AB=
| 12+32 |
| 10 |
∵∠ABO+∠EBC=∠ABO+∠BAO=∠BAO+∠DAG=∠DAG+∠ADG=90°,
∴∠EBC=∠BAO=∠ADG,
在△BEC和△AOB与△GDA中,
|
∴△BEC≌△AOB≌△GDA(AAS),
∴EC=OB=AG=3,BE=AO=DG=1,
∴OE=OB-BE=3-1=2,OG=AD-OA=3-1=2,
∴C(3,2),D(2,1).
点评:本题考查了正方形的性质的运用,勾股定理的运用,坐标于图形的性质的运用,解答时作辅助线制造直角三角形是重点,运用三角形全等求值是关键.

练习册系列答案
相关题目
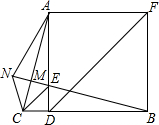 如图,已知正方形ADBF,点E在AD上,且∠AEB=105°,EC∥DF交BD的延长线于C,N为BE延长线上一点,BN交AC于M,且CE=2MN,连接AN、CN,下列结论:①AC⊥BN;②△NCE为等边三角形;③BF=2AM;④BE+
如图,已知正方形ADBF,点E在AD上,且∠AEB=105°,EC∥DF交BD的延长线于C,N为BE延长线上一点,BN交AC于M,且CE=2MN,连接AN、CN,下列结论:①AC⊥BN;②△NCE为等边三角形;③BF=2AM;④BE+ 如图,△ABC与△DBC能够完全重合,则△ABC与△DBC是
如图,△ABC与△DBC能够完全重合,则△ABC与△DBC是 如图,已知△ABC的∠ABC=80°,∠C=70°;将△ABC顺时针旋转至△AB′C′,B′C′边恰好过点B,则图中的∠1=
如图,已知△ABC的∠ABC=80°,∠C=70°;将△ABC顺时针旋转至△AB′C′,B′C′边恰好过点B,则图中的∠1=