Question

7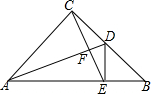．如图所示，△ABC是等腰直角三角形，∠ACB=90°，AD是BC边上的中线，过C作AD的垂线，交AB于点E，交AD于点F．
求证：（1）∠ADC=∠BDE；（用两种方法证明）
（2）CE+DE=AD．

Answer 1

分析 （1）作CH⊥AB于H交AD于P，根据已知条件求得△APH≌△CEH（ASA），△PDC≌△EDB（SAS），根据全等三角形的性质即可得到结论；
（2）首先根据全等三角形的判定得出△ACP≌△BCE以及△DCP≌△DBE，根据全等三角形的性质即可得到结论．

解答 证明：（1）作CH⊥AB于H交AD于P，
∵在Rt△ABC中，AC=CB，∠ACB=90°，
∴∠CAB=∠CBA=45°，
∴∠HCB=90°-∠CBA=45°=∠CBA，
又∵BC中点为D，
∴CD=BD，
又∵CH⊥AB，
∴CH=AH=BH，
又∵∠PAH+∠APH=90°，∠PCF+∠CPF=90°，∠APH=∠CPF，
∴∠PAH=∠ECH，
在△APH与△CEH中，$\left\{\begin{array}{l}{∠PAH=∠HCE}\\{AH=CH}\\{∠PHA=∠EHC}\end{array}\right.$，
∴△APH≌△CEH（ASA），
∴PH=EH，
又∵PC=CH-PH，BE=BH-HE，
∴CP=EB，
∵△ACB是等腰直角三角形，
∴∠B=45°，
即∠EBD=45°，
∵CH⊥AB，
∴∠PCD=45°=∠EBD，
在△PDC与△EDB中，$\left\{\begin{array}{l}{PC=BE}\\{∠PCD=∠EBD}\\{DC=DB}\end{array}\right.$，
∴△PDC≌△EDB（SAS），
∴∠ADC=∠BDE；
（2）∵∠ACD=90°，∠AFC=90°，
∴∠ADC=∠ACF，
∵等腰直角三角形△ABC中，∠ACB=90°，CH是AB上的高，
∴AC=BC，CH=AH=BH，∠CAH=∠ACH=∠BCH=∠B=45°，
∵CE⊥AD，∴∠BCE+∠ACF=∠CAD+∠ACF=90°，
∴∠BCE=∠CAD
在△ACP和△BCE中，
$\left\{\begin{array}{l}{∠ACH=∠B}\\{AC=BC}\\{∠CAD=∠BCE}\end{array}\right.$
∴△ACP≌△BCE（ASA），
∴AP=CE，
∵点D是BC的中点，∴CD=BD．
在△DCP和△DBE中，
$\left\{\begin{array}{l}{CP=BE}\\{∠DCP=∠B}\\{CD=BD}\end{array}\right.$，
∴△DCP≌△DBE（SAS），
∴DP=DE，
∴AD=AP+PD=CE+DE．

点评 此题主要考查了等腰直角三角形的性质以及全等三角形的判定与性质，根据已知得出△ACG≌△BCE是解题关键．