题目内容
如图（1），从正方体的3个不同方向圴匀地各切1刀，可得8个小正方体；如图（2），从正方体的3个不同方向均匀地各切2刀，可得27个小正方体；…
那么，沿正方体的3个不同方向均匀地各切n刀，得到正方体的个数应该为______．
解：∵8=（1+1）3；
27=（2+1）3，
根据规律可得：沿正方体的3个不同方向均匀地各切n刀，得到正方体的个数应该为 （n+1）3．
故答案是：（n+1）3．
分析：根据已知条件猜想切的刀数与正方体的个数的关系，根据规律即可求解．
点评：本题考查了图形的变化规律，关键是理解8=（1+1）3，27=（2+1）3．
27=（2+1）3，
根据规律可得：沿正方体的3个不同方向均匀地各切n刀，得到正方体的个数应该为 （n+1）3．
故答案是：（n+1）3．
分析：根据已知条件猜想切的刀数与正方体的个数的关系，根据规律即可求解．
点评：本题考查了图形的变化规律，关键是理解8=（1+1）3，27=（2+1）3．
练习册系列答案
阅读快车系列答案
相关题目
如图一只蚂蚁要从正方体一个顶点A爬到另一个顶点B，如果正方体棱长是2，求最短路线长．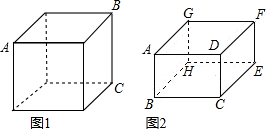
一只蚂蚁在立方体的表面积爬行．