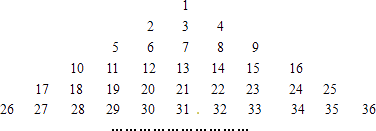��Ŀ����
����Ŀ����ͼ��������![]() ���̵ع���һ��յأ���߳�Ϊ
���̵ع���һ��յأ���߳�Ϊ![]() �ף�����Ʋ���Ϊ�˸���ͯ�ṩ�����ʡ�����ȫ�Ļ���أ������յ��е��ı���
�ף�����Ʋ���Ϊ�˸���ͯ�ṩ�����ʡ�����ȫ�Ļ���أ������յ��е��ı���![]() ������Ϊ��ͯ���������Χ��Χ��������ֻ����������ڣ�����
������Ϊ��ͯ���������Χ��Χ��������ֻ����������ڣ�����![]() ����
����![]() ����
����![]() �����Ҹ���ʵ����Ҫ��Ҫʹ��
�����Ҹ���ʵ����Ҫ��Ҫʹ��![]() ��������ͯ��������ı���
��������ͯ��������ı���![]() ������Ϊ
������Ϊ![]() ��
��![]() ���ֲ�ͬ����Ϸ���أ���ͯ���֮��IJ�����ֲ���ݣ�
���ֲ�ͬ����Ϸ���أ���ͯ���֮��IJ�����ֲ���ݣ�
��![]() ����ֱ��д���߶�
����ֱ��д���߶�![]() ��
�� ![]() ��
�� ![]() ֮���������ϵ��__________��
֮���������ϵ��__________��
��![]() ����ͼ�ڣ���
����ͼ�ڣ���![]() �ף���������ͯ����������
�ף���������ͯ����������
��![]() �������Ƿ����һ����Ʒ�����ʹ�ö�ͯ����������������ڣ��������ͯ�����������ֵ���������ڣ���˵�����ɣ�
�������Ƿ����һ����Ʒ�����ʹ�ö�ͯ����������������ڣ��������ͯ�����������ֵ���������ڣ���˵�����ɣ�

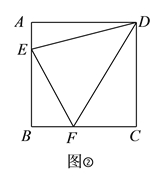

���𰸡�![]()
����������![]() ������ת������֤������������ȫ�ȣ����ɵó��߶�
������ת������֤������������ȫ�ȣ����ɵó��߶�![]() ��
�� ![]() ��
�� ![]() ֮���������ϵ����
֮���������ϵ����![]() ��ͬ��1���ɵ�
��ͬ��1���ɵ�![]() �����ù��ɶ������a��������ö�ͯ������������
�����ù��ɶ������a��������ö�ͯ������������![]() ������ֱ��ƽ���Ƴ�����ʽ���Ӷ��ó���ͯ�����������
������ֱ��ƽ���Ƴ�����ʽ���Ӷ��ó���ͯ�����������
�⣺������![]() �߳�
�߳�![]() ��
�� ![]() ��
��
��![]() ����
����![]() ��ת
��ת![]() ��
��![]() ��
��![]() �غϣ�
�غϣ�
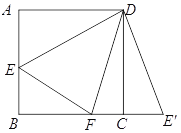
��֤![]() ��
��![]() ��
��
��![]() ��
��
��![]() ��ͬ������
��ͬ������![]() ��ת��
��ת��![]() ��
��
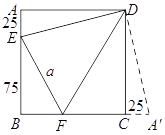
ͬ�ϣ���ʱ![]() ��
�� ![]() ��
�� ![]() ��
��
![]() ��
��![]() ��
��
![]() ��
��
��![]() ��
��
��![]() ��
��![]() ��
��
��![]() ʱ��
ʱ�� ![]() ��
��
![]() ��
��
![]() ��
��
![]() ��
��
![]() ��
��
![]() ��
��
��![]() ��
��
![]() ��
��

��ϰ��ϵ�д�
�����Ŀ