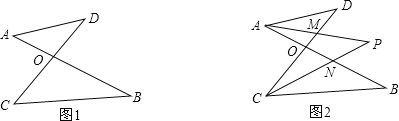题目内容
【题目】将线段![]() 绕点
绕点![]() 逆时针旋转角度
逆时针旋转角度![]() 得到线段
得到线段![]() ,连接
,连接![]() 得
得![]() ,又将线段
,又将线段![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得线段
得线段![]() (如图①).
(如图①).
![]() 求
求![]() 的大小(结果用含
的大小(结果用含![]() 的式子表示);
的式子表示);
![]() 又将线段
又将线段![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 得线段
得线段![]() ,连接
,连接![]() (如图②)求
(如图②)求![]() ;
;
![]() 连接
连接![]() 、
、![]() ,试探究当
,试探究当![]() 为何值时,
为何值时,![]() .
.

【答案】(1)![]() ;(2)
;(2)![]() ; (3) 当
; (3) 当![]() 为
为![]() 时,
时,![]() .
.
【解析】
(1)由于线段AB绕点A逆时针旋转角度α(0°<α<60°)得到线段AC,根据旋转的性质得AB=AC,∠BAC=α,利用等腰三角形的性质和三角形内角和定理得到![]() 再由线段BC绕点B逆时针旋转60°得线段BD,根据旋转的性质得∠CBD=60°,然后利用∠ABD=∠ABC-∠CBD进行计算;
再由线段BC绕点B逆时针旋转60°得线段BD,根据旋转的性质得∠CBD=60°,然后利用∠ABD=∠ABC-∠CBD进行计算;
(2)由线段AB绕点B顺时针旋转60°得线段BE,根据旋转的性质得AB=AE,∠BAE=60°,则AC=AE,∠CAE=60°-α,利用等腰三角形的性质和三角形内角和得到![]() 然后利用∠BCE=∠ACB+∠ACE计算得到∠BCE=150°;
然后利用∠BCE=∠ACB+∠ACE计算得到∠BCE=150°;
(3)由线段BC绕点B逆时针旋转60°得线段BD,根据旋转的性质得BC=BD,∠CBD=60°,则可判断△BCD为等腰直角三角形,则∠BCD=60°,CD=BC,
所以∠DCE=∠BCE-∠BCD=90°,加上∠DEC=45°,于是△DEC为等腰直角三角形,则CE=CD,所以CB=CE,然后利用“SSS”证明△ABC≌△AEC,得到∠BAC=∠EAC,所以![]()
![]() ∵线段
∵线段![]() 绕点
绕点![]() 逆时针旋转角度
逆时针旋转角度![]() 得到线段
得到线段![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵线段![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得线段
得线段![]() ,
,
∴![]() ,
,
∴![]() ;
;

![]() ∵线段
∵线段![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 得线段
得线段![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ;
;![]() 如图②,
如图②,
∵线段![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得线段
得线段![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() 为等边三角形,
为等边三角形,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() 为等腰直角三角形,
为等腰直角三角形,
∴![]() ,
,
∴![]() ,
,
在![]() 和
和![]() 中
中
 ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
即![]() ,
,
当![]() 为
为![]() 时,
时,![]() .
.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案
相关题目