题目内容
3.解不等式:(1)$\frac{x+5}{2}-1<\frac{3x+2}{2}$
(2)$\left\{\begin{array}{l}x+3>0\\ 2(x-1)+3≥3x\end{array}\right.$.
分析 (1)不等式去分母,去括号,移项合并,把x系数化为1,即可求出解集;
(2)分别求出不等式组中两不等式的解集,找出解集的公共部分即可.
解答 解:(1)去分母得:x+5-2<3x+2,
移项合并得:2x>1,
解得:x>$\frac{1}{2}$;
(2)$\left\{\begin{array}{l}{x+3>0①}\\{2(x-1)+3≥3x②}\end{array}\right.$,
由①得:x>-3,
由②得:x≤1,
则不等式组的解集为-3<x≤1.
点评 此题考查了解一元一次不等式组,以及解一元一次不等式,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
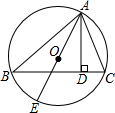 如图所示,△ABC内接于⊙O,AD⊥BC于点D,AE是⊙O的直径.
如图所示,△ABC内接于⊙O,AD⊥BC于点D,AE是⊙O的直径.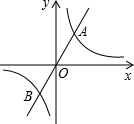 如图,正比例函数y1=k1x和反比例函数y2=$\frac{k2}{x}$的图象交于A(1,2),B两点,给出下列结论:①k1<k2;②当x<-1时,y1<y2;③当y1>y2时,y2随x的增大而减小;④当x<0时,y2随x的增大而减小.其中正确的有( )
如图,正比例函数y1=k1x和反比例函数y2=$\frac{k2}{x}$的图象交于A(1,2),B两点,给出下列结论:①k1<k2;②当x<-1时,y1<y2;③当y1>y2时,y2随x的增大而减小;④当x<0时,y2随x的增大而减小.其中正确的有( )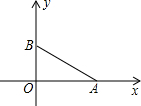 如图,在直角坐标系中有两点A(4,0),B(0,2)如果C在x轴上(C点与A不重合),当C点坐标为(-1,0) 或(1,0)时,使得由点B,O,C构成的三角形与△AOB相似(至少找出两个满足条件点).
如图,在直角坐标系中有两点A(4,0),B(0,2)如果C在x轴上(C点与A不重合),当C点坐标为(-1,0) 或(1,0)时,使得由点B,O,C构成的三角形与△AOB相似(至少找出两个满足条件点).