题目内容
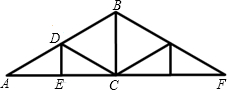
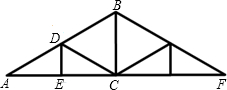
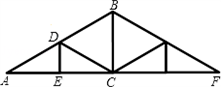
如图是等腰三角形屋架设计图的一部分,点D是斜梁AB的中点,立柱BC,DE垂直于横梁AC,AB=8m,∠A=30°,求:
(1)∠ABF的度数;
(2)立柱BC,DE要多长.
解:(1)∠ABF=180°﹣2×30°=120°.
故∠ABF的度数为120°;
(2)∵立柱BC、DE垂直于横梁AC,
∴BC∥DE,
∵D是AB中点,
∴AD=BD,
∴AE:CE=AD:BD,
∴AE=CE,
∴DE是△ABC的中位线,
∴DE= BC,
BC,
在Rt△ABC中,
BC= AB=4m,
AB=4m,
∴DE=2m.
故立柱BC长4m,DE长2m.
故∠ABF的度数为120°;
(2)∵立柱BC、DE垂直于横梁AC,
∴BC∥DE,
∵D是AB中点,
∴AD=BD,
∴AE:CE=AD:BD,
∴AE=CE,
∴DE是△ABC的中位线,
∴DE=
 BC,
BC,在Rt△ABC中,
BC=
 AB=4m,
AB=4m,∴DE=2m.
故立柱BC长4m,DE长2m.

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案
相关题目