题目内容
10.将抛物线y=ax2+2ax+3绕原点旋转180°后所得的抛物线与x轴交于(1,0),则a的值是3.分析 根据“关于原点对称的两点的横坐标纵坐标都互为相反数”即可得到抛物线y=ax2+2ax+3经过点(-1,0),将其代入该函数解析式列出关于a的方程,通过解方程来求a的值.
解答 解:∵抛物线y=ax2+2ax+3绕原点旋转180°后所得的抛物线与x轴交于(1,0),
∴抛物线y=ax2+2ax+3经过点(-1,0),
∴a-2a+3=0,
解得a=3.
故答案是:3.
点评 本题考查了二次函数图象与几何变换.根据已知条件得到抛物线y=ax2+2ax+3经过点(-1,0)是解题的突破口.

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
1.下列四组线段中,不能构成直角三角形的是( )
| A. | 4,5,6 | B. | 3,4,5 | C. | 5,12,13 | D. | 7,24,25 |
20.一个正方体的体积为25,估计这个正方形的边长在( )
| A. | 2和3之间 | B. | 3和4之间 | C. | 4和5之间 | D. | 5和6之间 |
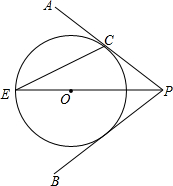 如图,点O在∠APB的平分线上,⊙O与PA相切于点C.
如图,点O在∠APB的平分线上,⊙O与PA相切于点C. 已知:如图,在平面直角坐标系中,有菱形OABC,点A的坐标为(10,0),对角线OB、AC相交于点D,双曲线y=$\frac{k}{x}$(x>0)经过点D,交BC的延长线于点E,且OB•AC=160,有下列四个结论:
已知:如图,在平面直角坐标系中,有菱形OABC,点A的坐标为(10,0),对角线OB、AC相交于点D,双曲线y=$\frac{k}{x}$(x>0)经过点D,交BC的延长线于点E,且OB•AC=160,有下列四个结论: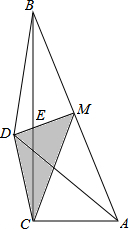 在△ABC中,AB=13,BC=12,CA=5,M是AB中点,点D与C在AB同侧,使DA=DB=7,则△CDM的面积为$\frac{357\sqrt{3}}{104}$.
在△ABC中,AB=13,BC=12,CA=5,M是AB中点,点D与C在AB同侧,使DA=DB=7,则△CDM的面积为$\frac{357\sqrt{3}}{104}$.