题目内容
如图,AB是半圆O的直径,F是半圆上一点,D是OA上一点,过点D作ED⊥AB,交半圆于点C,交B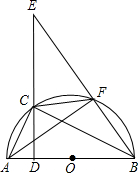 F的延长线于点E,连接AC,AF,BC.
F的延长线于点E,连接AC,AF,BC.
(1)求证:∠E=∠BCF;
(2)求证:BC2=BF•BE;
(3)若BC=12,CF=6,BF=9,求sin∠AFC.
(1)证明:∵∠1=∠2,∠AFB=90°,
∴∠2+∠ABF=90°;
∵∠ABF+∠E=90°,
∴∠E=∠1,即∠E=∠BCF;
(2)证明:在△BCE与△BFC中,∠E=∠BCF,∠CBF=∠CBF;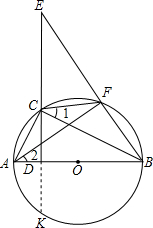
故△BCE∽△BFC,∴ =
= ,即BC2=BF•BE;
,即BC2=BF•BE;
(3)解:将半圆补全,延长ED,交⊙O于K.
∵BC2=BF•BE,BC=12,BF=9;
∴BE=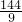 ;
;
∴CE=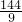 ×
× ×6=
×6=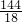 =8;
=8;
∴EF=EB-FB=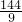 -9=
-9=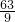 =7;
=7;
∵EF•EB=EC•EK,即7×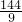 =8×(8+2CD);解得CD=3.
=8×(8+2CD);解得CD=3.
在Rt△BCD中,BC=12;因此sin∠DBC= =
=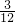 =
= .
.
又因为∠AFC=∠DBC,所以sin∠AFC= .
.
分析:(1)根据圆周角定理可得∠1=∠2,由于AB是半圆O的直径,所以∠AFB=90°,即∠2+∠ABF=90°;由于ED⊥AB,所以∠E+∠ABF=90°;故∠E=∠2=∠1,即∠E=∠BCF.
(2)由(1)可知∠E=∠BCF,因为∠CBF=∠CBF,故△BCE∽△BFC;
根据相似三角形的性质即可求出BC2=BF•BE.
(3)将圆补全,利用割线定理解答.
点评:此题是一道圆与相似三角形结合的题目,主要考查同学们的综合运用能力.
∴∠2+∠ABF=90°;
∵∠ABF+∠E=90°,
∴∠E=∠1,即∠E=∠BCF;
(2)证明:在△BCE与△BFC中,∠E=∠BCF,∠CBF=∠CBF;

故△BCE∽△BFC,∴
 =
= ,即BC2=BF•BE;
,即BC2=BF•BE;(3)解:将半圆补全,延长ED,交⊙O于K.
∵BC2=BF•BE,BC=12,BF=9;
∴BE=
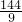 ;
;∴CE=
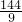 ×
× ×6=
×6=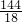 =8;
=8;∴EF=EB-FB=
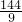 -9=
-9=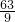 =7;
=7;∵EF•EB=EC•EK,即7×
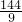 =8×(8+2CD);解得CD=3.
=8×(8+2CD);解得CD=3.在Rt△BCD中,BC=12;因此sin∠DBC=
 =
=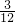 =
= .
.又因为∠AFC=∠DBC,所以sin∠AFC=
 .
.分析:(1)根据圆周角定理可得∠1=∠2,由于AB是半圆O的直径,所以∠AFB=90°,即∠2+∠ABF=90°;由于ED⊥AB,所以∠E+∠ABF=90°;故∠E=∠2=∠1,即∠E=∠BCF.
(2)由(1)可知∠E=∠BCF,因为∠CBF=∠CBF,故△BCE∽△BFC;
根据相似三角形的性质即可求出BC2=BF•BE.
(3)将圆补全,利用割线定理解答.
点评:此题是一道圆与相似三角形结合的题目,主要考查同学们的综合运用能力.

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案
相关题目
 如图,AB是半圆O的直径,AC是弦,点P从点B开始沿BA边向点A以1cm/s的速度移动,若AB长为10cm,点O到AC的距离为4cm.
如图,AB是半圆O的直径,AC是弦,点P从点B开始沿BA边向点A以1cm/s的速度移动,若AB长为10cm,点O到AC的距离为4cm. 已知:如图,AB是半圆O的直径,OD是半径,BM切半圆于点B,OC与弦AD平行交BM于点C.
已知:如图,AB是半圆O的直径,OD是半径,BM切半圆于点B,OC与弦AD平行交BM于点C. 如图,AB是半圆O的直径,点D是半圆上一动点,AB=10,AC=8,当△ACD是等腰三角形时,点D到AB的距离是
如图,AB是半圆O的直径,点D是半圆上一动点,AB=10,AC=8,当△ACD是等腰三角形时,点D到AB的距离是 如图,AB是半圆O的直径,以OA为直径的半圆O′与弦AC交于点D,O′E∥AC,并交OC于点E,则下列结论:①S△O′OE=
如图,AB是半圆O的直径,以OA为直径的半圆O′与弦AC交于点D,O′E∥AC,并交OC于点E,则下列结论:①S△O′OE=
