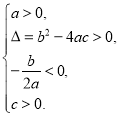题目内容
【题目】方方驾驶小汽车匀速地从![]() 地行驶到
地行驶到![]() 地,行驶里程为
地,行驶里程为![]() 千米,设小汽车的行驶时间为
千米,设小汽车的行驶时间为![]() (单位:小时),行驶速度为
(单位:小时),行驶速度为![]() (单位:千米/小时),且全程速度限定为不超过
(单位:千米/小时),且全程速度限定为不超过![]() 千米/小时.
千米/小时.
(1)求![]() 关于
关于![]() 的函数表达式,并写出自变量
的函数表达式,并写出自变量![]() 的取值范围;
的取值范围;
(2)方方上午![]() 点驾驶小汽车从
点驾驶小汽车从![]() 地出发;
地出发;
①方方需在当天![]() 点
点![]() 分至
分至![]() 点(含
点(含![]() 点
点![]() 分和
分和![]() 点)间到达
点)间到达![]() 地,求小汽车行驶速度
地,求小汽车行驶速度![]() 的范围;
的范围;
②方方能否在当天![]() 点
点![]() 分前到达
分前到达![]() 地?说明理由.
地?说明理由.
【答案】(1)![]() ;(2)①
;(2)①![]() ;②方方不能在当天
;②方方不能在当天![]() 点
点![]() 分前到达
分前到达![]() 地.
地.
【解析】
(1)由速度乘以时间等于路程,变形即可得速度等于路程比时间,从而得解;
(2)①8点至12点48分时间长为![]() 小时,8点至14点时间长为6小时,将它们分别代入v关于t的函数表达式,即可得小汽车行驶的速度范围;
小时,8点至14点时间长为6小时,将它们分别代入v关于t的函数表达式,即可得小汽车行驶的速度范围;
②8点至11点30分时间长为![]() 小时,将其代入v关于t的函数表达式,可得速度大于120千米/时,从而得答案.
小时,将其代入v关于t的函数表达式,可得速度大于120千米/时,从而得答案.
解:(1) ![]() ,且全程速度限定为不超过120千米/时,
,且全程速度限定为不超过120千米/时,
![]()
![]() 关于
关于![]() 的函数表达式为:
的函数表达式为:![]() .
.
(2)①![]() 点至
点至![]() 点
点![]() 分时间长为
分时间长为![]() 小时,
小时,![]() 点至
点至![]() 点时间长为
点时间长为![]() 小时
小时
将![]() 代入
代入![]() 得
得![]() ;
;
将![]() 代入
代入![]() 得,
得,![]()
![]() 小汽车行驶速度
小汽车行驶速度![]() 的范围为:
的范围为:![]() .
.
②方方不能在当天![]() 点
点![]() 分前到达
分前到达![]() 地.理由如下:
地.理由如下:
![]() 点至
点至![]() 点
点![]() 分时间长为
分时间长为![]() 小时,
小时,
将![]() 代入
代入![]() 中,
中,
得![]() 千米/时,超速了.
千米/时,超速了.
所以方方不能在当天![]() 点
点![]() 分前到达
分前到达![]() 地.
地.

 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案【题目】关于![]() 的一元二次方程
的一元二次方程![]() 有两个不相等且非零的实数根,探究
有两个不相等且非零的实数根,探究![]() 满足的条件.
满足的条件.
小华根据学习函数的经验,认为可以从二次函数的角度研究一元二次方程的根的符号。下面是小华的探究过程:第一步:设一元二次方程![]() 对应的二次函数为
对应的二次函数为![]() ;
;
第二步:借助二次函数图象,可以得到相应的一元二次方程中![]() 满足的条件,列表如下表。
满足的条件,列表如下表。
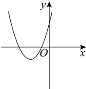
方程两根的情况 | 对应的二次函数的大致图象 |
|
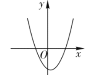
方程有两个不相等的负实根 |
|
|
①_______ |
|
|
方程有两个不相等的正实根 | ② | ③____________ |
(1)请将表格中①②③补充完整;
(2)已知关于![]() 的方程
的方程![]() ,若方程的两根都是正数,求
,若方程的两根都是正数,求![]() 的取值范围.
的取值范围.