题目内容
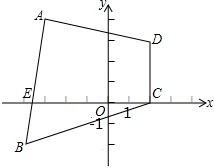 如图,在平面直角坐标系中,四边形ADCB各顶点的坐标分别是A(-3,4)、D(2,3)、C(2,0)、B(-4,-2),且AB与x轴交点E的坐标为 (-
如图,在平面直角坐标系中,四边形ADCB各顶点的坐标分别是A(-3,4)、D(2,3)、C(2,0)、B(-4,-2),且AB与x轴交点E的坐标为 (-| 11 |
| 3 |
考点:坐标与图形性质,三角形的面积
专题:
分析:过点A作AF⊥EC于F,根据点A的坐标求出点F的坐标,然后根据S四边形ABCD=S△AEF+S△EBC+S梯形AFCD,列式进行计算即可得解.
解答: 解:如图,过点A作AF⊥EC于F,
解:如图,过点A作AF⊥EC于F,
∵A(-3,4),
∴F(-3,0),
S四边形ABCD=S△AEF+S△EBC+S梯形AFCD
=
×4×(
-3)+
×(
+2)×2+
×(4+3)×(2+3)
=
+
+
=24
.
 解:如图,过点A作AF⊥EC于F,
解:如图,过点A作AF⊥EC于F,∵A(-3,4),
∴F(-3,0),
S四边形ABCD=S△AEF+S△EBC+S梯形AFCD
=
| 1 |
| 2 |
| 11 |
| 3 |
| 1 |
| 2 |
| 11 |
| 3 |
| 1 |
| 2 |
=
| 4 |
| 3 |
| 17 |
| 3 |
| 35 |
| 2 |
=24
| 1 |
| 2 |
点评:本题考查了坐标与图形性质,三角形面积,作辅助线,把不规则图形转化为几个规则图形的面积的和是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
某校九年级(2)班40名同学这“希望工程”捐款,共捐款100元,捐款情况如下表:
表格中捐款2元和3元的人数不小心被墨水污染已看不清楚,若设捐款2元的有x名同学,捐款3元的有y名同学,假设(x,y)是两个一次函数图象的交点,则这两个一次函数解析式分别是( )
| 捐款(元) | 1 | 2 | 3 | 4 |
| 人数 | 6 |  |
7 | |
A、y=27-x与y=-
| ||||
B、y=27-x与y=-
| ||||
C、y=27-x与y=-
| ||||
D、y=27-x与y=-
|
函数y=-
的图象经过的点是( )
| 2 |
| x |
| A、(-1,2) | ||
| B、(-1,-2) | ||
| C、(2,1) | ||
D、(-
|
 如图所示,每一个小方格都是边长为1的单位正方形.△ABC的三个顶点都在格点上,以点O为坐标原点建立平面直角坐标系.
如图所示,每一个小方格都是边长为1的单位正方形.△ABC的三个顶点都在格点上,以点O为坐标原点建立平面直角坐标系. 如图,∠A与
如图,∠A与