题目内容
3.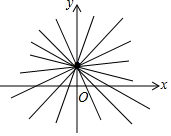 当k取不同的值时,y关于x的函数y=kx+1(k≠0)的图象为总是经过点(0,1)的直线,我们把所有这样的直线合起来,称为经过点(0,1)的“直线束”.那么,下面经过点(-1,1)的直线束的函数式是( )
当k取不同的值时,y关于x的函数y=kx+1(k≠0)的图象为总是经过点(0,1)的直线,我们把所有这样的直线合起来,称为经过点(0,1)的“直线束”.那么,下面经过点(-1,1)的直线束的函数式是( )| A. | y=kx-1(k≠0) | B. | y=kx+k+1(k≠0) | C. | y=kx-k+1(k≠0) | D. | y=kx+k-1(k≠0) |
分析 把点(-1,1)分别代入下面点解析式,根据一次函数图象上点点坐标特征判断即可.
解答 解:A、x=-1时,y=-k-1≠1,故不经过点(-1,1);
B、x=-1时,y=-k+k+1=1,故经过点(-1,1);
C、x=-1时,y=-k-k+1≠1,故不经过点(-1,1);
D、x=-1时,y=-k+k-1≠1,故不经过点(-1,1);
故选B.
点评 本题考查了一次函数图象上点的坐标特征,图象上点符合解析式上解题的关键.

练习册系列答案
相关题目
13. 如图,将?ABCD沿对角线AC折叠,使点B落在点B'处.若∠1=∠2=44°,则∠B为( )
如图,将?ABCD沿对角线AC折叠,使点B落在点B'处.若∠1=∠2=44°,则∠B为( )
 如图,将?ABCD沿对角线AC折叠,使点B落在点B'处.若∠1=∠2=44°,则∠B为( )
如图,将?ABCD沿对角线AC折叠,使点B落在点B'处.若∠1=∠2=44°,则∠B为( )| A. | 124° | B. | 114° | C. | 104° | D. | 66° |
14.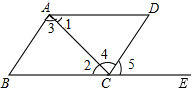 如图,四边形ABCD中,点E在BC延长线上,则下列条件中不能判断AB∥CD的是( )
如图,四边形ABCD中,点E在BC延长线上,则下列条件中不能判断AB∥CD的是( )
 如图,四边形ABCD中,点E在BC延长线上,则下列条件中不能判断AB∥CD的是( )
如图,四边形ABCD中,点E在BC延长线上,则下列条件中不能判断AB∥CD的是( )| A. | ∠3=∠4 | B. | ∠1=∠2 | C. | ∠5=∠ABC | D. | ∠1+∠3+∠D=180° |
11.某校八年级有800名学生,从中随机抽取了100名学生进行立定跳远测试,其中说法错误的是( )
| A. | 这种调查方式是抽样调查 | |
| B. | 每名学生的立定跳远成绩是个体 | |
| C. | 100名学生是样本容量 | |
| D. | 这100名学生的立定跳远成绩是总体的一个样本 |
8.在下面几何体中,其俯视图是三角形的是( )
| A. |  | B. |  | C. |  | D. |  |
15.某幢楼10户家庭每月的用电量如下表所示:
那么这10户家庭该月用电量的众数和中位数分别是( )
| 用电量(度) | 140 | 160 | 180 | 200 |
| 户数 | 1 | 3 | 4 | 2 |
| A. | 180,180 | B. | 180,160 | C. | 160,180 | D. | 160,160 |
12.如果向东走50m记为50m,那么向西走30m记为( )
| A. | -30m | B. | |-30|m | C. | -(-30)m | D. | $\frac{1}{30}$m |
13.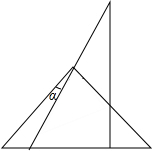 一副三角板如图叠放在一起,则图中∠α的度数为( )
一副三角板如图叠放在一起,则图中∠α的度数为( )
 一副三角板如图叠放在一起,则图中∠α的度数为( )
一副三角板如图叠放在一起,则图中∠α的度数为( )| A. | 35° | B. | 30° | C. | 25° | D. | 15° |
 如图,已知扇形AOB中,OA=3,∠AOB=120°,C是在$\widehat{AB}$上的动点.以BC为边作正方形BCDE,当点C从点A移动至点B时,点D经过的路径长是2$\sqrt{2}$π.
如图,已知扇形AOB中,OA=3,∠AOB=120°,C是在$\widehat{AB}$上的动点.以BC为边作正方形BCDE,当点C从点A移动至点B时,点D经过的路径长是2$\sqrt{2}$π.