题目内容
【题目】如图,已知△ABC是面积为 ![]() 的等边三角形,△ABC∽△ADE,AB=2AD,∠BAD=45°,AC与DE相交于点F,则△AEF的面积等于(结果保留根号).
的等边三角形,△ABC∽△ADE,AB=2AD,∠BAD=45°,AC与DE相交于点F,则△AEF的面积等于(结果保留根号). 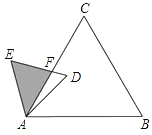
【答案】![]()
【解析】解:∵△ABC∽△ADE,AB=2AD, ∴ ![]() =
= ![]() ,
,
∵AB=2AD,S△ABC= ![]() ,
,
∴S△ADE= ![]() ,
,
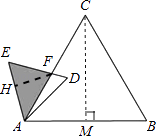
如图,在△EAF中,过点F作FH⊥AE交AE于H,
∵∠EAF=∠BAD=45°,∠AEF=60°,
∴∠AFH=45°,∠EFH=30°,
∴AH=HF,
设AH=HF=x,则EH=xtan30°= ![]() x.
x.
又∵S△ADE= ![]() ,
,
作CM⊥AB交AB于M,
∵△ABC是面积为 ![]() 的等边三角形,
的等边三角形,
∴ ![]() ×AB×CM=
×AB×CM= ![]() ,
,
∠BCM=30°,
设AB=2k,BM=k,CM= ![]() k,
k,
∴k=1,AB=2,
∴AE= ![]() AB=1,
AB=1,
∴x+ ![]() x=1,
x=1,
解得x= ![]() =
= ![]() .
.
∴S△AEF= ![]() ×1×
×1× ![]() =
= ![]() .
.
所以答案是: ![]() .
.
【考点精析】认真审题,首先需要了解等边三角形的性质(等边三角形的三个角都相等并且每个角都是60°),还要掌握相似三角形的性质(对应角相等,对应边成比例的两个三角形叫做相似三角形)的相关知识才是答题的关键.

练习册系列答案
相关题目