Question

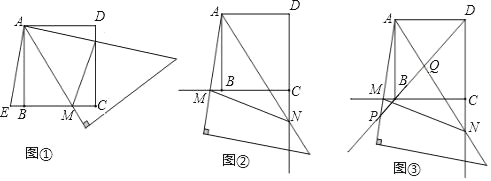
【题目】如图，在△ABC中，AD⊥BC于D，BD＝AD，DG＝DC．

（1）求证：△BDG≌△ADC．

（2）分别取BG、AC的中点E、F，连接DE、DF，则DE与DF有何关系，并说明理由．

（3）在（2）的条件下，连接EF，若AC＝10，求EF的长．

Answer 1

【答案】（1）详见解析；（2）详见解析；（3）

【解析】

（1）由∠ADB=∠ADC=90°，BD=AD，DG=DC，即可得；

（2）由△BDG≌△ADC，根据全等三角形的性质、直角三角形的性质即可得到DE=DF，DE⊥DF；

（3）根据直角三角形的性质分别求出DE、DF，根据勾股定理计算即可．

（1）∵AD⊥BC，

∴∠ADB=∠ADC=90°，

又∵BD=AD，DG=DC，

∴△BDG≌△ADC；

（2）DE=DF，DE⊥DF，理由如下：

∵△BDG≌△ADC，

∴BG=AC,∠EBD=∠FAD，

∵∠ADB=∠ADC=90°，E，F分别是BG，AC的中点，

∴，

∴DE=DF，

∵ DE=BE ，

∴∠EBD=∠EDB，

∵ DF=BF，

∴∠FDA=∠FAD，

∴∠EDB=∠FDA，

∵∠EDB+∠EDG=∠ADB=90°，

∴∠FDA+∠EDG=90°，

∴DE⊥DF；

(3) ∵AC=10，∠ADC=90°，BG、AC的中点E、F，

∴DE=DF=5，

由（2）知，△DEF是等腰直角三角形，

由勾股定理得，.