题目内容
如图,OA⊥OB,等腰直角三角形CDE的腰CD在OB上,∠ECD=45°,将三角形CDE绕点C逆时针旋转75°,点E的对应点N恰好落在OA上,则 的值为( )
的值为( )

 的值为( )
的值为( )
A. |
B. |
C. |
D. |
C
根据旋转得出∠NCE=75°,求出∠NCO,设OC=a,则CN=2a,根据△CMN也是等腰直角三角形设CM=MN=x,由勾股定理得出x2+x2=(2a)2,求出x=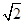 a,得出CD=
a,得出CD=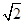 a,代入求出即可.
a,代入求出即可.
解:∵将三角形CDE绕点C逆时针旋转75°,点E的对应点N恰好落在OA上,
∴∠ECN=75°,
∵∠ECD=45°,
∴∠NCO=180°﹣75°﹣45°=60°,
∵AO⊥OB,
∴∠AOB=90°,
∴∠ONC=30°,

设OC=a,则CN=2a,
∵等腰直角三角形DCE旋转到△CMN,
∴△CMN也是等腰直角三角形,
设CM=MN=x,则由勾股定理得:x2+x2=(2a)2,
x=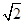 a,
a,
即CD=CM=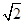 a,
a,
∴ =
=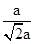 =
= ,
,
故选C.
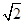 a,得出CD=
a,得出CD=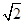 a,代入求出即可.
a,代入求出即可.解:∵将三角形CDE绕点C逆时针旋转75°,点E的对应点N恰好落在OA上,
∴∠ECN=75°,
∵∠ECD=45°,
∴∠NCO=180°﹣75°﹣45°=60°,
∵AO⊥OB,
∴∠AOB=90°,
∴∠ONC=30°,

设OC=a,则CN=2a,
∵等腰直角三角形DCE旋转到△CMN,
∴△CMN也是等腰直角三角形,
设CM=MN=x,则由勾股定理得:x2+x2=(2a)2,
x=
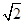 a,
a,即CD=CM=
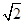 a,
a,∴
 =
=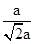 =
= ,
,故选C.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
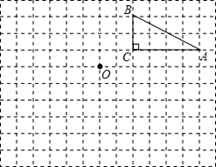
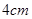 的等边△ABC沿边
的等边△ABC沿边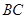 向右平移2cm得到△
向右平移2cm得到△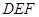 ,则四边形ABFD的周长为 .
,则四边形ABFD的周长为 .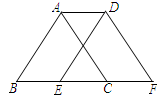

 ,1),B(1,
,1),B(1,

