题目内容
 如图,AB是半圆O的直径,AB=10,过点A的直线交半圆于点C,且AC=6,连结BC,点D为BC的中点.已知点E在直线AC上,△CDE与△ACB相似,则线段AE的长为________.
如图,AB是半圆O的直径,AB=10,过点A的直线交半圆于点C,且AC=6,连结BC,点D为BC的中点.已知点E在直线AC上,△CDE与△ACB相似,则线段AE的长为________.
3或 或9或
或9或
分析:根据E点在直线AC上,得出对应点不同求出的EC长度不同,分别得出即可.
解答: 解:∵AB是半圆O的直径,
解:∵AB是半圆O的直径,
∴∠ACB=90°,
∵AB=10,AC=6,
∴BC= =8,
=8,
∵点D为BC的中点,
∴CD=4,
当DE∥AB时,
△CED∽△CAB,
∴ =
= ,
,
∴ =
=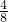 ,
,
解得:EC=3,
∴AE=6-EC=3,
当 =
= ,且∠ACB=∠DCE′时,△CE′D∽△CBA,
,且∠ACB=∠DCE′时,△CE′D∽△CBA,
则 =
= ,
,
解得:CE′= ,
,
∴AE′=6- =
= ;
;
当 =
= ,且∠ACB=∠DCE1时,△CE1D∽△CBA,
,且∠ACB=∠DCE1时,△CE1D∽△CBA,
则 =
= ,
,
解得:CE1= ,
,
∴AE1=6+ =
= ;
;
当 =
= ,且∠ACB=∠DCE″时,△CE″D∽△CBA,
,且∠ACB=∠DCE″时,△CE″D∽△CBA,
则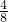 =
= ,
,
解得:CE″=3,
∴AE″=6+3=9;
综上所述:点E在直线AC上,△CDE与△ACB相似,则线段AE的长为3或 或9或
或9或 .
.
故答案为:3或 或9或
或9或 .
.
点评:此题主要考查了相似三角形的判定与性质,注意在直线AC上有一点E,进行分类讨论得出是解题关键.
 或9或
或9或
分析:根据E点在直线AC上,得出对应点不同求出的EC长度不同,分别得出即可.
解答:
 解:∵AB是半圆O的直径,
解:∵AB是半圆O的直径,∴∠ACB=90°,
∵AB=10,AC=6,
∴BC=
 =8,
=8,∵点D为BC的中点,
∴CD=4,
当DE∥AB时,
△CED∽△CAB,
∴
 =
= ,
,∴
 =
=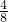 ,
,解得:EC=3,
∴AE=6-EC=3,
当
 =
= ,且∠ACB=∠DCE′时,△CE′D∽△CBA,
,且∠ACB=∠DCE′时,△CE′D∽△CBA,则
 =
= ,
,解得:CE′=
 ,
,∴AE′=6-
 =
= ;
;当
 =
= ,且∠ACB=∠DCE1时,△CE1D∽△CBA,
,且∠ACB=∠DCE1时,△CE1D∽△CBA,则
 =
= ,
,解得:CE1=
 ,
,∴AE1=6+
 =
= ;
;当
 =
= ,且∠ACB=∠DCE″时,△CE″D∽△CBA,
,且∠ACB=∠DCE″时,△CE″D∽△CBA,则
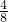 =
= ,
,解得:CE″=3,
∴AE″=6+3=9;
综上所述:点E在直线AC上,△CDE与△ACB相似,则线段AE的长为3或
 或9或
或9或 .
.故答案为:3或
 或9或
或9或 .
.点评:此题主要考查了相似三角形的判定与性质,注意在直线AC上有一点E,进行分类讨论得出是解题关键.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
 如图,AB是半圆O的直径,AC是弦,点P从点B开始沿BA边向点A以1cm/s的速度移动,若AB长为10cm,点O到AC的距离为4cm.
如图,AB是半圆O的直径,AC是弦,点P从点B开始沿BA边向点A以1cm/s的速度移动,若AB长为10cm,点O到AC的距离为4cm. 已知:如图,AB是半圆O的直径,OD是半径,BM切半圆于点B,OC与弦AD平行交BM于点C.
已知:如图,AB是半圆O的直径,OD是半径,BM切半圆于点B,OC与弦AD平行交BM于点C. 如图,AB是半圆O的直径,点D是半圆上一动点,AB=10,AC=8,当△ACD是等腰三角形时,点D到AB的距离是
如图,AB是半圆O的直径,点D是半圆上一动点,AB=10,AC=8,当△ACD是等腰三角形时,点D到AB的距离是 如图,AB是半圆O的直径,以OA为直径的半圆O′与弦AC交于点D,O′E∥AC,并交OC于点E,则下列结论:①S△O′OE=
如图,AB是半圆O的直径,以OA为直径的半圆O′与弦AC交于点D,O′E∥AC,并交OC于点E,则下列结论:①S△O′OE=
