题目内容
5.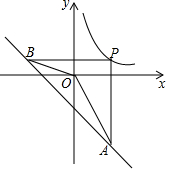 如图,P为反比例函数y=$\frac{k}{x}$(x>0)在第一象限内图象上的一点,过点P分别作x轴、y轴的垂线交一次函数y=-x-2的图象于点A、B.若AO、BO分别平分∠BAP、∠ABP,则k的值为2.
如图,P为反比例函数y=$\frac{k}{x}$(x>0)在第一象限内图象上的一点,过点P分别作x轴、y轴的垂线交一次函数y=-x-2的图象于点A、B.若AO、BO分别平分∠BAP、∠ABP,则k的值为2.
分析 如图,连接OP,作AM⊥y轴于M,设A交y轴于N.首先证明OP是第一象限是角平分线,设P(a,a),则A(a,-a-2),B(-a-2,a),可得PB=2a+2,PA=2a+2,推出PA=PB,推出∠PBA=∠PAB=45°,推出∠OAN=∠OAP=∠AON=22.5°,推出∠ANM=∠NOA+∠NAO=45°,推出AM=MN=a,AN=ON=$\sqrt{2}$a,推出A(a,-a-$\sqrt{2}$a),可得方程-a-$\sqrt{2}$a=-a-2,由此即可解决问题.
解答 解:如图,连接OP,作AM⊥y轴于M,设A交y轴于N.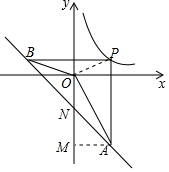
∵AO、BO分别平分∠BAP、∠ABP,
∴点O是△PAB的内心,
∴OP平分∠APB,
∵∠APB=90°,
∴∠OPA=∠OPB=45°,
∴OP是第一象限是角平分线,设P(a,a),则A(a,-a-2),B(-a-2,a),
∴PB=2a+2,PA=2a+2,
∴PA=PB,
∴∠PBA=∠PAB=45°,
∴∠OAN=∠OAP=∠AON=22.5°,
∴∠ANM=∠NOA+∠NAO=45°,
∴AM=MN=a,AN=ON=$\sqrt{2}$a,
∴A(a,-a-$\sqrt{2}$a),
∴-a-$\sqrt{2}$a=-a-2,
∴a=$\sqrt{2}$,
∴P($\sqrt{2}$,$\sqrt{2}$),
∵点P在y=$\frac{k}{x}$上,
∴k=2,
故答案为2.
点评 本题考查三角形的内心、反比例函数、一次函数、等腰直角三角形的性质等知识,解题的关键是灵活运用所学知识解决问题,学会利用参数解决问题,属于中考常填空题中的压轴题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16.如图是某单位考核情况条形统计图(A、B、C三个等级),则下面的回答正确的是( )
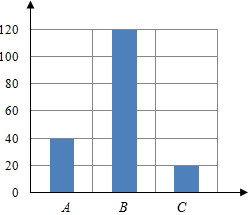

| A. | C等人最少,占总数的30% | B. | 该单位共有120人 | ||
| C. | A等人比C等多10% | D. | B等人最多,占总人数的$\frac{2}{3}$ |
10.四边形ABCD是正方形,以CD为边向正方形外作正△CDE,则∠EAB的度数为( )
| A. | 75° | B. | 72° | C. | 67.5° | D. | 65° |
14.力帆集团原计划生产某一型号的汽车8000辆,为了提高效率,企业改进了技术,现每天可比原计划多生产40辆汽车,结果提前10天完成了生产计划.若设原计划需要x天完成,则根据题意列方程为( )
| A. | $\frac{8000}{x}$-$\frac{8000}{x+10}$=40 | B. | $\frac{8000}{x+10}$-$\frac{8000}{x}$=40 | ||
| C. | $\frac{8000}{x-10}$=$\frac{8000}{x}$+40 | D. | $\frac{8000}{x-10}$=$\frac{8000}{x}$-40 |
 如图,已知a∥b,∠1=46°,则∠2等于=134°.
如图,已知a∥b,∠1=46°,则∠2等于=134°.
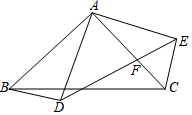 如图△ABC与△ADE都是以A为直角顶点的等腰直角三角形,DE交AC于点F.
如图△ABC与△ADE都是以A为直角顶点的等腰直角三角形,DE交AC于点F.