题目内容
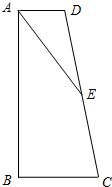 如图,在梯形ABCD中,AD∥BC,点E为CD上一点,且DE=EC=BC.
如图,在梯形ABCD中,AD∥BC,点E为CD上一点,且DE=EC=BC.
(1)若∠B=90°,求证:∠AEC=3∠DAE;
(2)若tan∠DAE= ,AD=2,AE=5,求梯形ABCD的面积.
,AD=2,AE=5,求梯形ABCD的面积.
(1)证明:延长AE交BC的延长线于F,连接BE,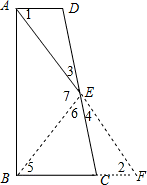
∵AD∥BC,
∴∠1=∠2,
在△ADE和△FCE中,
∵
∴△ADE≌△FCE,
∴AE=EF,
又∵△ABF为直角三角形,
∴BE=EF,
∴∠5=∠2=∠1,
∴∠7=2∠1,
又∵CE=BC,
∴∠5=∠6=∠1,
∴∠AEC=∠6+∠7=3∠1,
即∠AEC=3∠DAE.
(2)解:过D作DH⊥AE于H,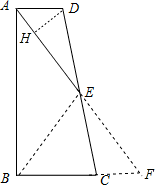
由(1)SABCD=S△ABF=2S△BEF,
∵在Rt△ADH中,tan∠DAH= ,
,
∴sin∠DAE= =
=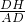 ,
,
即 =
= ,
,
∴DH= ,
,
∵tan∠DAE= =
=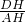 ,
,
∴AH= ,
,
∴S△ADE= ×AE×DH=
×AE×DH= ×5×
×5× =4,
=4,
∴S△ECF=4,
∵AE=5,AH= ,
,
∴HE=5- =
=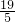 ,
,
在Rt△DHE中,由勾股定理得:DE= ,
,
即BC=DE= ,
,
∵CF=AD=2,
∴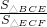 =
=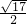 ,
,
∴S△BCE=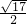 ×4=2
×4=2 ,
,
∴S△EBF=2 +4,
+4,
∴S△ABF=2S△EBF=4 +8,
+8,
即S梯形ABCD=4 +8.
+8.
分析:(1)延长AE交BC的延长线于F,连接BE,证△ADE≌△FCE,推出AE=EF,根据等腰三角形性质求出∠5=∠2=∠1,推出∠7=2∠1,根据等腰三角形性质得出∠5=∠6=∠1,求出∠AEC=∠6+∠7=3∠1即可;
(2)过D作DH⊥AE于H,由(1)SABCD=S△ABF=2S△BEF,根据tan∠DAH= 求出DH=
求出DH= 、AH=
、AH= ,求出S△ADE=S△ECF=4,由勾股定理求出DE=
,求出S△ADE=S△ECF=4,由勾股定理求出DE= ,求出BC=DE=
,求出BC=DE= ,根据三角形面积公式求出S△BCE,求出S△EBF=2
,根据三角形面积公式求出S△BCE,求出S△EBF=2 +4,求出S△ABF=4
+4,求出S△ABF=4 +8,即可求出梯形面积.
+8,即可求出梯形面积.
点评:本题考查了全等三角形的性质和判定,梯形的面积,三角形的面积,三角形的外角性质,勾股定理解直角三角形等知识点的综合运用,题目综合性比较强,难度偏大.

∵AD∥BC,
∴∠1=∠2,
在△ADE和△FCE中,
∵

∴△ADE≌△FCE,
∴AE=EF,
又∵△ABF为直角三角形,
∴BE=EF,
∴∠5=∠2=∠1,
∴∠7=2∠1,
又∵CE=BC,
∴∠5=∠6=∠1,
∴∠AEC=∠6+∠7=3∠1,
即∠AEC=3∠DAE.
(2)解:过D作DH⊥AE于H,

由(1)SABCD=S△ABF=2S△BEF,
∵在Rt△ADH中,tan∠DAH=
 ,
,∴sin∠DAE=
 =
=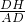 ,
,即
 =
= ,
,∴DH=
 ,
,∵tan∠DAE=
 =
=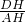 ,
,∴AH=
 ,
,∴S△ADE=
 ×AE×DH=
×AE×DH= ×5×
×5× =4,
=4,∴S△ECF=4,
∵AE=5,AH=
 ,
,∴HE=5-
 =
=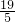 ,
,在Rt△DHE中,由勾股定理得:DE=
 ,
,即BC=DE=
 ,
,∵CF=AD=2,
∴
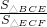 =
=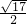 ,
,∴S△BCE=
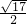 ×4=2
×4=2 ,
,∴S△EBF=2
 +4,
+4,∴S△ABF=2S△EBF=4
 +8,
+8,即S梯形ABCD=4
 +8.
+8.分析:(1)延长AE交BC的延长线于F,连接BE,证△ADE≌△FCE,推出AE=EF,根据等腰三角形性质求出∠5=∠2=∠1,推出∠7=2∠1,根据等腰三角形性质得出∠5=∠6=∠1,求出∠AEC=∠6+∠7=3∠1即可;
(2)过D作DH⊥AE于H,由(1)SABCD=S△ABF=2S△BEF,根据tan∠DAH=
 求出DH=
求出DH= 、AH=
、AH= ,求出S△ADE=S△ECF=4,由勾股定理求出DE=
,求出S△ADE=S△ECF=4,由勾股定理求出DE= ,求出BC=DE=
,求出BC=DE= ,根据三角形面积公式求出S△BCE,求出S△EBF=2
,根据三角形面积公式求出S△BCE,求出S△EBF=2 +4,求出S△ABF=4
+4,求出S△ABF=4 +8,即可求出梯形面积.
+8,即可求出梯形面积.点评:本题考查了全等三角形的性质和判定,梯形的面积,三角形的面积,三角形的外角性质,勾股定理解直角三角形等知识点的综合运用,题目综合性比较强,难度偏大.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,在梯形ABCD中,AD∥BC,∠BCD=90°,以CD为直径的半圆O切AB于点E,这个梯形的面积为21cm2,周长为20cm,那么半圆O的半径为( )
如图,在梯形ABCD中,AD∥BC,∠BCD=90°,以CD为直径的半圆O切AB于点E,这个梯形的面积为21cm2,周长为20cm,那么半圆O的半径为( )| A、3cm | B、7cm | C、3cm或7cm | D、2cm |
 11、如图,在梯形ABCD中,AB∥CD,对角线AC、BD交于点O,则S△AOD
11、如图,在梯形ABCD中,AB∥CD,对角线AC、BD交于点O,则S△AOD 已知:如图,在梯形ABCD中,AD∥BC,AB⊥BC,AD=2,BC=CD=10.
已知:如图,在梯形ABCD中,AD∥BC,AB⊥BC,AD=2,BC=CD=10. 如图,在梯形ABCD中,AD∥BC,AB⊥AD,对角线BD⊥DC.
如图,在梯形ABCD中,AD∥BC,AB⊥AD,对角线BD⊥DC. 20、如图,在梯形ABCD中,AD∥BC,并且AB=8,AD=3,CD=6,并且∠B+∠C=90°,则梯形面积S梯形ABCD=
20、如图,在梯形ABCD中,AD∥BC,并且AB=8,AD=3,CD=6,并且∠B+∠C=90°,则梯形面积S梯形ABCD=