题目内容
14.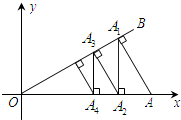 如图,在平面直角坐标系中,∠AOB=30°,点A坐标为(2,0),过A作AA1⊥OB,垂足为点A1;过点A1作A1A2⊥x轴,垂足为点A2;再过点A2作A2A3⊥OB,垂足为点A3;则A2A3=$\frac{3}{4}$;再过点A3作A3A4⊥x轴,垂足为点A4…;这样一直作下去,则A2017的纵坐标为$(\frac{\sqrt{3}}{2})^{2017}$.
如图,在平面直角坐标系中,∠AOB=30°,点A坐标为(2,0),过A作AA1⊥OB,垂足为点A1;过点A1作A1A2⊥x轴,垂足为点A2;再过点A2作A2A3⊥OB,垂足为点A3;则A2A3=$\frac{3}{4}$;再过点A3作A3A4⊥x轴,垂足为点A4…;这样一直作下去,则A2017的纵坐标为$(\frac{\sqrt{3}}{2})^{2017}$.
分析 根据含30°的直角三角形的性质结合图形即可得到规律“OAn=$(\frac{\sqrt{3}}{2})^{n}$OA=2$(\frac{\sqrt{3}}{2})^{n}$”,依此规律即可解决问题.
解答 解:∵∠AOB=30°,点A坐标为(2,0),
∴OA=2,
∴OA1=$\frac{\sqrt{3}}{2}$OA=$\sqrt{3}$,OA2=$\frac{\sqrt{3}}{2}$OA1═$\frac{3}{2}$,OA3=$\frac{\sqrt{3}}{2}$OA2═$\frac{3\sqrt{3}}{4}$,OA4=$\frac{\sqrt{3}}{2}$OA3═$\frac{9}{8}$,…,
∴OAn=$(\frac{\sqrt{3}}{2})^{n}$OA=2$(\frac{\sqrt{3}}{2})^{n}$.
∵∠AOB=30°,
∴A2A3=$\frac{1}{2}$OA2=$\frac{3}{4}$,
∴A2017A2018=$\frac{1}{2}$OA2017=$(\frac{\sqrt{3}}{2})^{2017}$.
故答案为:$\frac{3}{4}$;$(\frac{\sqrt{3}}{2})^{2017}$.
点评 本题考查了规律型中点的坐标以及含30度角的直角三角形,利用“在直角三角形中,30°角所对的直角边等于斜边的一半”结合图形找出变化规律OAn=$(\frac{\sqrt{3}}{2})^{n}$OA=2$(\frac{\sqrt{3}}{2})^{n}$是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7.下列方程组中是二元一次方程组的是( )
| A. | $\left\{\begin{array}{l}{x-y=3}\\{xy=1}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{2x+y=5}\\{x=3y-2}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{{x}^{2}-y=1}\\{y=2x}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{\frac{1}{y}-\frac{1}{x}=2}\\{x+y=0}\end{array}\right.$ |
9.在(-1)2017,(-3)0,$\sqrt{9}$,($\frac{1}{2}$)-2,这四个数中,最大的数是( )
| A. | (-1)2017 | B. | (-3)0 | C. | $\sqrt{9}$ | D. | ($\frac{1}{2}$)-2 |
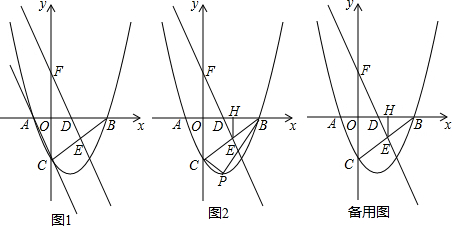
6. 如图所示的二次函数y=ax2+bx+c的图象中,刘星同学观察得出了下面四条信息:(1)b2-4ac>0;(2)c>1;(3)b<0;(4)a+b+c<0.你认为其中错误的有( )
如图所示的二次函数y=ax2+bx+c的图象中,刘星同学观察得出了下面四条信息:(1)b2-4ac>0;(2)c>1;(3)b<0;(4)a+b+c<0.你认为其中错误的有( )
 如图所示的二次函数y=ax2+bx+c的图象中,刘星同学观察得出了下面四条信息:(1)b2-4ac>0;(2)c>1;(3)b<0;(4)a+b+c<0.你认为其中错误的有( )
如图所示的二次函数y=ax2+bx+c的图象中,刘星同学观察得出了下面四条信息:(1)b2-4ac>0;(2)c>1;(3)b<0;(4)a+b+c<0.你认为其中错误的有( )| A. | 2个 | B. | 3个 | C. | 4个 | D. | 1个 |
3.若x=0是关于x的一元二次方程(a+2)x2-$\sqrt{a-2}$x+a2+a-6=0的一个根,则a的值是( )
| A. | a≠-2 | B. | a=2 | C. | a=-3 | D. | a=-3或a=2 |
 如图所示,共有线段6条,共有射线7条.
如图所示,共有线段6条,共有射线7条.