题目内容
 如图,直线y=kx+b,与抛物线y=ax2交于A(1,m),B(-2,4)+y轴交与点C.
如图,直线y=kx+b,与抛物线y=ax2交于A(1,m),B(-2,4)+y轴交与点C.(1)求抛物线的解析式;
(2)求S△AOB;
(3)求
| BC | AC |
(4)判断点A是否在以BO为直径的圆上?并说明理由.
分析:(1)把点B代入抛物线解析式求出a的值,即可得解;
(2)把点A代入抛物线解析式求出m,得到点A的坐标,过点A作AE⊥x轴于E,过点B作BF⊥x轴于F,根据S△AOC=S梯形ABFE-S△AOE-S△BOF,列式计算即可得解;
(3)根据平行线分线段成比例定理解答即可;
(4)利用待定系数法求一次函数解析式求出直线AB的解析式,得到∠ACO=45°,再根据点A的坐标求出∠AOC=45°,然后求出∠OAC=90°,然后根据直径所对的圆周角是直角证明即可.
(2)把点A代入抛物线解析式求出m,得到点A的坐标,过点A作AE⊥x轴于E,过点B作BF⊥x轴于F,根据S△AOC=S梯形ABFE-S△AOE-S△BOF,列式计算即可得解;
(3)根据平行线分线段成比例定理解答即可;
(4)利用待定系数法求一次函数解析式求出直线AB的解析式,得到∠ACO=45°,再根据点A的坐标求出∠AOC=45°,然后求出∠OAC=90°,然后根据直径所对的圆周角是直角证明即可.
解答:解:(1)∵抛物线y=ax2经过点B(-2,4),
∴4a=4,
∴a=1,
∴抛物线的解析式为y=x2;
(2)把点A(1,m)代入y=x2得m=1,
∴点A的坐标为(1,1),
如图,过点A作AE⊥x轴于E,过点B作BF⊥x轴于F,
S△AOB=S梯形ABFE-S△AOE-S△BOF,
=
×(1+4)×(1+2)-
×1×1-
×2×4,
=
-
-4,
=3;
(3)∵AE⊥x轴,BF⊥x轴,OC⊥x轴,
∴AE∥BF∥OC,
∴
=
=2;
(4)∵直线y=kx+b经过A(1,1),B(-2,4),
∴
,
解得
,
∴直线AB的解析式为y=-x+2,
∵直线AB与y轴交与点C,
∴∠ACO=45°,
∵点A(1,1),
∴∠AOC=45°,
∴∠OAC=180°-45°-45°=90°,
∴点A在以BO为直径的圆上.
∴4a=4,
∴a=1,
∴抛物线的解析式为y=x2;
(2)把点A(1,m)代入y=x2得m=1,
∴点A的坐标为(1,1),

如图,过点A作AE⊥x轴于E,过点B作BF⊥x轴于F,
S△AOB=S梯形ABFE-S△AOE-S△BOF,
=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=
| 15 |
| 2 |
| 1 |
| 2 |
=3;
(3)∵AE⊥x轴,BF⊥x轴,OC⊥x轴,
∴AE∥BF∥OC,
∴
| BC |
| AC |
| OF |
| OE |
(4)∵直线y=kx+b经过A(1,1),B(-2,4),
∴
|
解得
|
∴直线AB的解析式为y=-x+2,
∵直线AB与y轴交与点C,
∴∠ACO=45°,
∵点A(1,1),
∴∠AOC=45°,
∴∠OAC=180°-45°-45°=90°,
∴点A在以BO为直径的圆上.
点评:本题是二次函数综合题型,主要利用了待定系数法求二次函数解析式,待定系数法求一次函数解析式,三角形的面积,以及直径所对的圆周角是直角是的性质,综合题,但难度不大.

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
 如图,直线y=kx+b经过点A(0,3),B(-2,0),则k的值为( )
如图,直线y=kx+b经过点A(0,3),B(-2,0),则k的值为( )| A、3 | ||
B、
| ||
C、
| ||
D、-
|
 如图,直线y=kx+b经过A(2,1),B(-1,-2)两点,则不等式
如图,直线y=kx+b经过A(2,1),B(-1,-2)两点,则不等式| 1 |
| 2 |
| A、x<2 |
| B、x>-1 |
| C、x<1或x>2 |
| D、-1<x<2 |
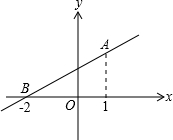 如图,直线y=kx+b经过A(1,2)和B(-2,0)两点,则不等式组-x+3≥kx+b>0的解集为
如图,直线y=kx+b经过A(1,2)和B(-2,0)两点,则不等式组-x+3≥kx+b>0的解集为 7、如图,直线y=kx+b和y=mx都经过点A(-1,-2),则不等式mx<kx+b的解集为( )
7、如图,直线y=kx+b和y=mx都经过点A(-1,-2),则不等式mx<kx+b的解集为( ) 16、如图,直线y=kx-1经过点(2,1),则不等式0≤x<2kx+2的解集为
16、如图,直线y=kx-1经过点(2,1),则不等式0≤x<2kx+2的解集为