题目内容
已知当x1=a,x2=b,x3=c时,二次函数y=x2+2mx对应的函数值分别为y1,y2,y3,若正整数a,b,c恰好是一个直角三角形的三边长,且当a<b<c时,都有y1<y2<y3,则实数m的取值范围是 .
考点:二次函数图象上点的坐标特征,勾股定理
专题:
分析:根据三角形的任意两边之和大于第三边和正整数a,b,c恰好是一个直角三角形的三边长,判断出a最小为3,再根据二次函数的增减性和对称性判断出对称轴在3、4之间偏向3,即不大于3.5,然后列出不等式求解即可.
解答:解:∵正整数a,b,c恰好是一个直角三角形的三边长,且a<b<c,
∴a最小是3,
∵y1<y2<y3,
∴-
<3.5,
解得m>-
.
故答案为:m>-
.
∴a最小是3,
∵y1<y2<y3,
∴-
| 2m |
| 2×1 |
解得m>-
| 7 |
| 2 |
故答案为:m>-
| 7 |
| 2 |
点评:本题考查了二次函数图象上点的坐标特征,三角形的三边关系,判断出a最小可以取3以及对称轴的位置是解题的关键.

练习册系列答案
相关题目
下列说法正确的是( )
| A、|a|一定不是负数 | ||||||
| B、|a|一定为正数 | ||||||
C、(-
| ||||||
| D、-|a|一定是负数 |
 如图,已知AB=DE,AC=DF,EC=BF,证明:AE=DB.
如图,已知AB=DE,AC=DF,EC=BF,证明:AE=DB.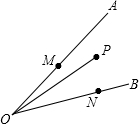 如图,已知∠AOB=30°,点P在∠AOB的内部,OP=6,若OA上有一动点M,OB上有一动点N,则△PMN的周长的最小值是
如图,已知∠AOB=30°,点P在∠AOB的内部,OP=6,若OA上有一动点M,OB上有一动点N,则△PMN的周长的最小值是