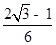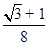题目内容
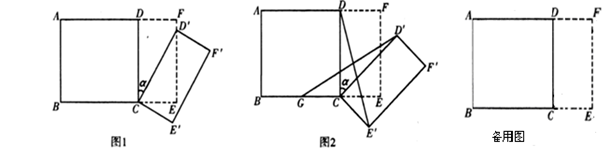
如图1所示,将一个边长为2的正方形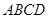 和一个长为2、宽为1的长方形
和一个长为2、宽为1的长方形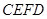 拼在一起,构成一个大的长方形
拼在一起,构成一个大的长方形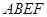 .现将小长方形
.现将小长方形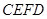 绕点
绕点 顺时针旋转至
顺时针旋转至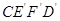 ,旋转角为
,旋转角为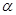 .
.
(1)当点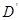 恰好落在
恰好落在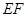 边上时,求旋转角
边上时,求旋转角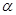 的值;
的值;
(2)如图2,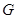 为
为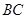 的中点,且0°<
的中点,且0°<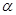 <90°,求证:
<90°,求证: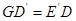 ;
;
(3)先将小长方形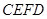 绕点
绕点 顺时针旋转,使
顺时针旋转,使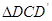 与
与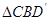 全等(0°<
全等(0°<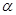 <180°),再将此时的小长方形
<180°),再将此时的小长方形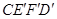 沿CD边竖直向上平移t个单位,设移动后小长方形边直线
沿CD边竖直向上平移t个单位,设移动后小长方形边直线 与BC交于点H,若DH∥FC,求上述运动变换过程中
与BC交于点H,若DH∥FC,求上述运动变换过程中 和t的值.
和t的值.
 和一个长为2、宽为1的长方形
和一个长为2、宽为1的长方形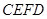 拼在一起,构成一个大的长方形
拼在一起,构成一个大的长方形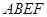 .现将小长方形
.现将小长方形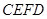 绕点
绕点 顺时针旋转至
顺时针旋转至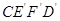 ,旋转角为
,旋转角为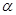 .
.(1)当点
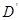 恰好落在
恰好落在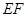 边上时,求旋转角
边上时,求旋转角 的值;
的值;(2)如图2,
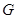 为
为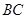 的中点,且0°<
的中点,且0°<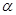 <90°,求证:
<90°,求证: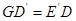 ;
;(3)先将小长方形
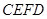 绕点
绕点 顺时针旋转,使
顺时针旋转,使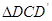 与
与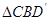 全等(0°<
全等(0°<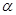 <180°),再将此时的小长方形
<180°),再将此时的小长方形 沿CD边竖直向上平移t个单位,设移动后小长方形边直线
沿CD边竖直向上平移t个单位,设移动后小长方形边直线 与BC交于点H,若DH∥FC,求上述运动变换过程中
与BC交于点H,若DH∥FC,求上述运动变换过程中 和t的值.
和t的值.
(1)α=30°; (2)证明见解析;(3)45°, -1.
-1.
 -1.
-1.试题分析:(1)根据题意知
 ,通过解直角三角形
,通过解直角三角形 ,即可求出
,即可求出 的值;
的值;(2)通过证明△GCD′≌△E′CD可得出结论;
(3)通过操作,易求出
 和t的值.
和t的值.(1) ∵DC//EF,
∴∠DCD′=∠CD′E=∠CD′E=α.
∴sinα=
 ,
,∴α=30°
(2) ∵G为BC中点,
∴GC=CE′=CE=1,
∵∠D′CG=∠DCG+∠DCD′=90°+α, ∠DCE′=∠D′CE′+∠DCD′=90°+α,
∴∠D′CG=∠DCE′又∵CD′=CD,
∴△GCD′≌△E′CD,
∴GD′=E′D.
α=135° 如图:

平移后,∵DH∥FC,AD∥BC,
∴四边形DHCF为平行四边形,
∴HC=DF=1,
题知:∠HGC=45°,GC′=

∴GC=HC=1,
∴矩形平移的路程t=CC′=
 -1.
-1.考点: 1.图形的旋转;2.三角函数;3.解直角三角形;4全等三角形的判定.

练习册系列答案
相关题目
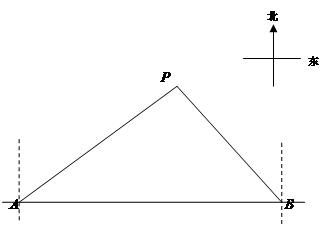
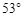 ,则秋千踏板与地面的最大距离约为多少?(参考数据:
,则秋千踏板与地面的最大距离约为多少?(参考数据: ≈0.8,
≈0.8, 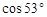 ≈0.6)
≈0.6)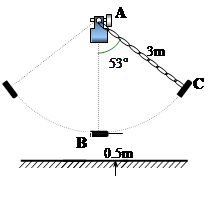

 ,且B、C、E三点在同一条直线上.
,且B、C、E三点在同一条直线上.






 ,则cosA的值为( )
,则cosA的值为( )



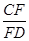 的值为( )
的值为( )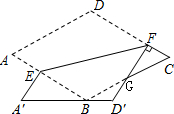
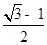
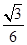 C.
C.