题目内容
定义新运算“⊕”如下:当a≥b时,a⊕b=ab-a;当a<b时,a⊕b=ab+b.
(1)计算:(-2)⊕ ;
;
(2)若2x⊕(x+1)=8,求x的值.
解:(1)(-2)⊕ =(-2)×
=(-2)× +
+ =1+
=1+ =
= ;
;
(2)当2x≥x+1时,
即:x≥1时,
2x(x+1)-2x=8,
解得:x=±2,
∵x≥1,
∴x=2;
当2x<x+1时,
即:x<1时,2x(x+1)+x+1=8,
2x2+3x-7=0
解得:x1=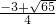 ,x2=
,x2=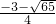 ,
,
∵x<1,
∴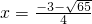 .
.
分析:(1)首先根据a⊕b=ab-a,认真分析找出规律,即可求出(-2)⊕ 的值;
的值;
(2)首先分两种情况进行讨论,当2x≥x+1和2x<x+1时,分别解出x的取值范围,即可得出x的值.
点评:此题考查了解一元二次方程-公式法,本题属于新定义题型,是近几年的考试热点之一.新定义题型需要依据给出的运算法则进行计算,这和解答实数或有理数的混合运算相同,其关键仍然是正确的理解与运用运算的法则.
 =(-2)×
=(-2)× +
+ =1+
=1+ =
= ;
;(2)当2x≥x+1时,
即:x≥1时,
2x(x+1)-2x=8,
解得:x=±2,
∵x≥1,
∴x=2;
当2x<x+1时,
即:x<1时,2x(x+1)+x+1=8,
2x2+3x-7=0
解得:x1=
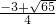 ,x2=
,x2=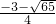 ,
,∵x<1,
∴
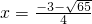 .
.分析:(1)首先根据a⊕b=ab-a,认真分析找出规律,即可求出(-2)⊕
 的值;
的值;(2)首先分两种情况进行讨论,当2x≥x+1和2x<x+1时,分别解出x的取值范围,即可得出x的值.
点评:此题考查了解一元二次方程-公式法,本题属于新定义题型,是近几年的考试热点之一.新定义题型需要依据给出的运算法则进行计算,这和解答实数或有理数的混合运算相同,其关键仍然是正确的理解与运用运算的法则.

练习册系列答案
相关题目