Question

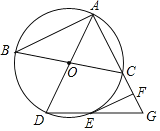
【题目】如图，∠BCD＝90°，且BC＝DC，直线PQ经过点D．设∠PDC＝α（45°＜α＜135°），BA⊥PQ于点A，将射线CA绕点C按逆时针方向旋转90°，与直线PQ交于点E．

（1）当α＝125°时，∠ABC＝　 　°；

（2）求证：AC＝CE；

（3）若△ABC的外心在其内部，直接写出α的取值范围．

Answer 1

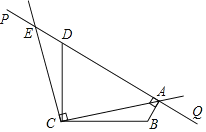
【答案】（1）125；（2）详见解析；（3）45°＜α＜90°．

【解析】

（1）利用四边形内角和等于360度得：∠B+∠ADC＝180°，而∠ADC+∠EDC＝180°，即可求解；

（2）证明△ABC≌△EDC（AAS）即可求解；

（3）当∠ABC＝α＝90°时，△ABC的外心在其直角边上，∠ABC＝α＞90°时，△ABC的外心在其外部，即可求解．

（1）在四边形BADC中，∠B+∠ADC＝360°﹣∠BAD﹣∠DCB＝180°，

而∠ADC+∠EDC＝180°，

∴∠ABC＝∠PDC＝α＝125°，

故答案为125；

（2）∠ECD+∠DCA＝90°，∠DCA+∠ACB＝90°，

∴∠ACB＝∠ECD，

又BC＝DC，由（1）知：∠ABC＝∠PDC，

∴△ABC≌△EDC（AAS），

∴AC＝CE；

（3）当∠ABC＝α＝90°时，△ABC的外心在其斜边上；∠ABC＝α＞90°时，△ABC的外心在其外部，而45°＜α＜135°，故：45°＜α＜90°．