题目内容
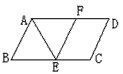
如图，?AECD中，AE平分∠DAB，∠B=120°，则∠DAE等于________°．
30
分析：由四边形AECD是平行四边形得出AD∥BC，根据两直线平行，同旁内角互补可得，∠DAB=180°-∠B=180°-120°=60°；根据角平分线的性质可得∠DAE=
∠DAB，将∠DAB的值代入即可求出∠DAE的值．
解答：∵四边形AECD是平行四边形
∴AD∥EC
即：AD∥BC
∴∠B+∠DAB=180°，∠DAB=180°-∠B=180°-120°=60°
又∵AE平分∠DAB
∴∠DAE=∠DAB=30°．
点评：本题考查平行四边形的性质结合平行线的性质来解决相关问题．用到的性质有：平行四边形的对边平行；两直线平行，同旁内角互补．
分析：由四边形AECD是平行四边形得出AD∥BC，根据两直线平行，同旁内角互补可得，∠DAB=180°-∠B=180°-120°=60°；根据角平分线的性质可得∠DAE=
∠DAB，将∠DAB的值代入即可求出∠DAE的值．解答：∵四边形AECD是平行四边形
∴AD∥EC
即：AD∥BC
∴∠B+∠DAB=180°，∠DAB=180°-∠B=180°-120°=60°
又∵AE平分∠DAB
∴∠DAE=
∠DAB=30°．点评：本题考查平行四边形的性质结合平行线的性质来解决相关问题．用到的性质有：平行四边形的对边平行；两直线平行，同旁内角互补．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
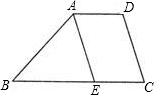
如图，?ABCD中，AE平分∠BAD交BC于E，EF∥AB交AD于F，试问：
如图，?ABCD中，AE平分∠BAD交BC于E，EF∥AB交AD于F，试问：
ABCD中，AE平分∠BAD 交BC于E，EF∥AB交AD于F，试问：