题目内容
9.据报道,某市浪费水现象严重,并且水资源极度匮乏,人均水资源占有量仅是全国人均占有量的$\frac{1}{3}$,世界人均占有量的$\frac{1}{15}$.(1)该市1年漏掉的水,相当于新建一个自来水厂,据不完全统计,全市至少有2.7×106个水龙头,6.4×105个抽水马桶漏水,如果关不紧的水龙头一天能漏掉am3的水,一个抽水马桶一天漏掉bm3的水,那么请你算出该市11月份造成的水流失量至少是多少?(用含a、b的代数式表示).
(2)水资源透支令人担忧,节约用水迫在眉睫.针对居民用水浪费现象,该市制定了居民用水标准,规定在楼房的3口之家每月标准用水量,超标部分加价收费.假设不超标部分每立方米水费为2.4元,超标部分每立方米水费为2.8元,某住楼房的3口之家某月用15m3,交水费38元,试求该市规定住楼房的3口之家每月标准用水量是多少?
分析 (1)根据题意,把所有水龙头漏掉的水和所有马桶漏掉的水相加即可;
(2)利用等量关系是不超标部分×2.4+超标部分×2.8=水费数,设该市规定住楼房的3口之家每月标准用水量是x立方米,则超标部分为(15-x)立方米,列方程即可解得.
解答 解:(1)2.7×106×30a+6.4×105×30a=8.1×107a+1.92×107b(m3).
答:11月份造成的水流失量至少是8.1×107a+1.92×107bm3.
(2)设该市规定住楼房的3口之家每月标准用水量是x立方米,由题意得
2.4x+2.8(15-x)=38,
解得:x=10.
答:该市规定住楼房的3口之家每月标准用水量是10m3.
点评 此题考查列代数式,一元一次方程的实际运用,理解题意,找出运算的方法以及数量关系解决问题.

练习册系列答案
 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目
19.在学校组织的魔方比赛中,小杰、小孙和小兰分别用了$\frac{7}{5}$分钟、$\frac{5}{3}$分钟、1.3分钟将魔方复原,根据比赛规则用时最短者获胜,那么获得冠军的应该是( )
| A. | 小杰 | B. | 小孙 | C. | 小兰 | D. | 无法确定 |
20.下列约分正确的是( )
| A. | $\frac{{x}^{6}}{{x}^{2}}$=x3 | B. | $\frac{x+y}{x+y}$=0 | C. | $\frac{x+y}{{x}^{2}+xy}$=$\frac{1}{x}$ | D. | $\frac{2x{y}^{2}}{2{x}^{2}y}$=$\frac{1}{2}$ |
1.如(2x+m)与(x-3)的乘积中不含x的一次项,则m的值为( )
| A. | -3 | B. | 3 | C. | -6 | D. | 6 |
18.两数相乘,积为负,则这两数( )
| A. | 都是正数 | B. | 都是负数 | C. | 一正一负 | D. | 不能确定 |
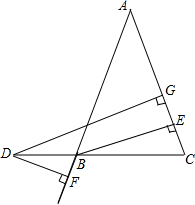 已知:如图,△ABC中,AB=AC,D是底边BC延长线上任意一点,且DG⊥AC,DF⊥AB,BE⊥AC,求证:BE=DG-DF.
已知:如图,△ABC中,AB=AC,D是底边BC延长线上任意一点,且DG⊥AC,DF⊥AB,BE⊥AC,求证:BE=DG-DF.