Question

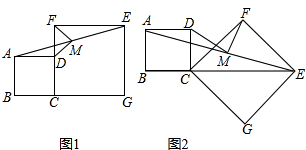
如图甲，在正方形ABCD和正方形CGEF（CG＞BC）中，点B、C、G在同一直线上，M是AE的中点．
（1）探究线段MD、MF的位置及数量关系，并证明；
（2）将图甲中的正方形CGEF绕点C顺时针旋转，使正方形CGEF的对角线CE恰好与正方形ABCD的边BC在同一直线上，原问题中的其他条件不变．（1）中得到的两个结论是否发生变化？写出你的猜想并加以证明．

Answer 1

考点：全等三角形的判定与性质,正方形的性质

专题：

分析：（1）延长DM交EF于点P，易证AM=EM，即可证明△ADM≌△EPM，可得DM=PM，根据△DFP是直角三角形即可解题；
（2）延长DM交CE于点N，连接FN、DF，易证∠DAM=∠NEM，即可证明△ADM≌△ENM，可得EN=AD，DM=MN，可证CD=EN，即可证明△CDF≌△ENF，可得DF=NF，即可解题．

解答：证明：（1）延长DM交EF于点P，

∵四边形ABCD和四边形FCGE是正方形，
∴AD∥EF，∠MAD=∠MEP．∠CFE=90°．
∴△DFP是直角三角形．
∵M为AE的中点，
∴AM=EM．
∵在△ADM和△EPM中，

∠MAD=∠MEP AM=EM ∠AMD=∠EMP

，
∴△ADM≌△EPM（ASA），
∴DM=PM．
∴M是DP的中点．
∴MF=

1

2

DP=MD；
（2）延长DM交CE于点N，连接FN、DF，

∵CE是正方形CFEG对角线，
∴∠FCN=∠CEF=45°，
∵∠DCE=90°，
∴∠DCF=45°，
∵AD∥BC，
∴∠DAM=∠NEM，
∵在△ADM和△ENM中，

∠DAM=∠NEM AM=EM ∠AMD=∠EMN

，
∴△ADM≌△ENM，（ASA）
∴EN=AD，DM=MN，
∵AD=CD，
∴CD=EN，
∵在△CDF和△ENF中，

CD=EN ∠DCF=∠CEF=45° CF=EF

，
∴△CDF≌△ENF，（SAS）
∴DF=NF，
∴FM=DM，FM⊥DM．

点评：本题考查了全等三角形的判定，考查了全等三角形对应边相等的性质，本题中求证△ADM≌△ENM和△CDF≌△ENF是解题的关键．