题目内容
 有一块形状为四边形的钢板,量得它的各边长度AB=3cm,AD=4cm,BC=13cm,CD=12cm,且∠A=90°,求这块钢板的面积.
有一块形状为四边形的钢板,量得它的各边长度AB=3cm,AD=4cm,BC=13cm,CD=12cm,且∠A=90°,求这块钢板的面积.分析:首先连接BD,利用勾股定理求出BD的长,再利用勾股定理逆定理得出∠BDC=90°,进而利用直角三角形面积求法得出即可.
解答: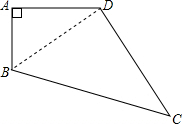 解:连接BD.
解:连接BD.
在Rt△ABD 中,由勾股定理得:BD=
=5(cm);
在△BCD 中,由BD2+CD2=52+122=BC2,
∴△BCD为Rt△,且∠BDC=90°
∴钢板的面积=
×AB×AD+
×BD×CD=
×3×4+
×5×12=36(cm2).
 解:连接BD.
解:连接BD.在Rt△ABD 中,由勾股定理得:BD=
| AB2+AD2 |
在△BCD 中,由BD2+CD2=52+122=BC2,
∴△BCD为Rt△,且∠BDC=90°
∴钢板的面积=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
点评:此题主要考查了勾股定理和勾股定理的逆定理等知识,得出∠BDC=90°是解题关键.

练习册系列答案
相关题目
 6、如图,小区的一角有一块形状为等腰梯形的空地,为了美化小区,社区居委会计划在空地上建一个四边形的水池,使水池的四个顶点恰好在梯形各边的中点上,则水池的形状一定是( )
6、如图,小区的一角有一块形状为等腰梯形的空地,为了美化小区,社区居委会计划在空地上建一个四边形的水池,使水池的四个顶点恰好在梯形各边的中点上,则水池的形状一定是( )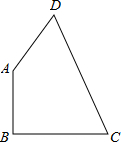 有一块形状为四边形的钢板,量得它的各边长度为AB=9cm,BC=12cm,CD=17cm,DA=8cm,∠B=90°.求这块钢板的面积.
有一块形状为四边形的钢板,量得它的各边长度为AB=9cm,BC=12cm,CD=17cm,DA=8cm,∠B=90°.求这块钢板的面积. 有一块形状为四边形的钢板,量得它的各边长度为AB=9cm,BC=12cm,CD=17cm,DA=8cm,∠B=90°.求这块钢板的面积.
有一块形状为四边形的钢板,量得它的各边长度为AB=9cm,BC=12cm,CD=17cm,DA=8cm,∠B=90°.求这块钢板的面积.