题目内容
17. 如图,△P1OA1,△P2A1A2,△P3A2A3,…,△PnAn-1An都是等腰直角三角形,点P1,P2,P3,…,Pn在函数y=$\frac{1}{x}$(x>0)的图象上,斜边OA1,A1A2,A2A3,…,An-1An都在x轴上,则点A1的坐标是(2,0),点A2016的坐标是(24$\sqrt{14}$,0).
如图,△P1OA1,△P2A1A2,△P3A2A3,…,△PnAn-1An都是等腰直角三角形,点P1,P2,P3,…,Pn在函数y=$\frac{1}{x}$(x>0)的图象上,斜边OA1,A1A2,A2A3,…,An-1An都在x轴上,则点A1的坐标是(2,0),点A2016的坐标是(24$\sqrt{14}$,0).
分析 分别作出点P1,P2,P3与x轴的垂线段,根据等腰直角三角形三线合一的性质可知,这此垂线段又是斜边上的中线,则等于斜边的一半;设未知数,根据反比例函数关系式列等量关系,求出未知数的值,并取舍,找出规律,并化简.
解答 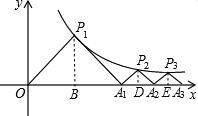 解:过点P1作P1B⊥x轴于B,
解:过点P1作P1B⊥x轴于B,
∵△P1OA1是等腰直角三角形,
∴OB=P1B,
则OB•P1B=1,
∴OB=1,OA1=2,
∴A1(2,0);
过点P2作P2D⊥x轴于D,设A1D=x,则OD=2+x,
同理得:A1D=P2D=x,
则OD•P2D=1,
x(2+x)=1,
解得:x1=-1+$\sqrt{2}$,x2=-1-$\sqrt{2}$(舍),
∴A2(2$\sqrt{2}$,0)
过点P3作P3E⊥x轴于E,设P3E=y,则OE=2$\sqrt{2}$+y,
则OE•P3E=1,
y(2$\sqrt{2}$+y)=1,
解得:y1=$\sqrt{3}$-$\sqrt{2}$,y2=-$\sqrt{2}-\sqrt{3}$(舍),
∴A2A3=2$\sqrt{3}$-2$\sqrt{2}$,
∴OA3=2$\sqrt{3}$-2$\sqrt{2}$+2$\sqrt{2}$=2$\sqrt{3}$,
∴A3(2$\sqrt{3}$,0),
所以可以得出:A2016的坐标(2$\sqrt{2016}$,0),即(24$\sqrt{14}$,0),
故答案为:(2,0),(24$\sqrt{14}$,0).
点评 本题主要考查了反比例函数图象上点的坐标特征,同时也考查了等腰直角三角形的性质;本题的关键是找出等腰直角三角形斜边上的中线等于斜边的一半,即点P1,P2,P3的纵坐标等于斜边的一半.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
8.某商店购进甲、乙两种商品共160件,甲每件进价15元,售价20元;乙每件进价为35元,售价45元;售完这批商品利润为1100元,则购进甲商品x件满足方程( )
| A. | 30x+15(160-x)=1100 | B. | 5(160-x)+10x=1100 | ||
| C. | 20x+25(160-x)=1100 | D. | 5x+10(160-x)=1100 |
5.计算:|1-$\sqrt{5}$|+|3-$\sqrt{5}$|-|3.14-π|=( )
| A. | 0.86-2$\sqrt{5}$+π | B. | 5.14-π | C. | 2$\sqrt{5}$-7.14+π | D. | -1.14+π |
12.已知二次函数y=a(x+1)(x-3)的最大值为8,则常数a为( )
| A. | -4 | B. | -3 | C. | -2 | D. | 2 |
9.若(a+2)2+|b-3|=0,则-ab的值是( )
| A. | 8 | B. | -8 | C. | -9 | D. | 9 |
6. 如图,在Rt△ABC中,∠ACB=90°,CD为AB边上的高,若点A关于CD所在直线的对称点E恰好为AB的中点,则∠A的度数为( )
如图,在Rt△ABC中,∠ACB=90°,CD为AB边上的高,若点A关于CD所在直线的对称点E恰好为AB的中点,则∠A的度数为( )
 如图,在Rt△ABC中,∠ACB=90°,CD为AB边上的高,若点A关于CD所在直线的对称点E恰好为AB的中点,则∠A的度数为( )
如图,在Rt△ABC中,∠ACB=90°,CD为AB边上的高,若点A关于CD所在直线的对称点E恰好为AB的中点,则∠A的度数为( )| A. | 30° | B. | 45° | C. | 60° | D. | 75° |
7.已知$\sqrt{{a}^{3}-0.125}$+(b3+64)2=0,则α+b的值是( )
| A. | -3.5 | B. | -3 | C. | -2.5 | D. | -2 |