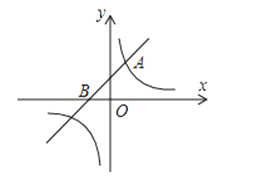题目内容
【题目】已知直线![]() 经过点
经过点![]() .
.
(1)求直线![]() 的解析式;
的解析式;
(2)把直线![]() 向右平移并与
向右平移并与![]() 轴相交于
轴相交于![]() 得到
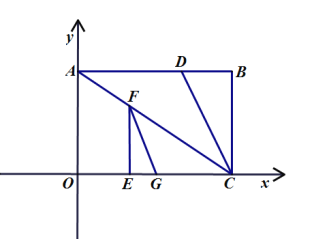
得到![]() ,请在如图所示平面直角坐标系中作出直线
,请在如图所示平面直角坐标系中作出直线![]() ;
;
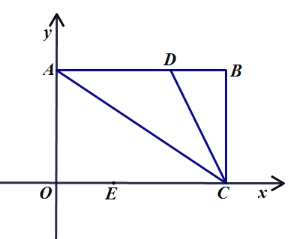
(3)若直线![]() 与
与![]() 轴交于
轴交于![]() 点,与直线
点,与直线![]() 交于点
交于点![]() ,求
,求![]() 的面积.
的面积.

【答案】(1)y=![]() x-3;(2)见解析;(3)4
x-3;(2)见解析;(3)4
【解析】
(1)设直线![]() 的解析式为y=kx+b,将点
的解析式为y=kx+b,将点![]() 代入,得到方程组,解出k,b即可;
代入,得到方程组,解出k,b即可;
(2)先画出直线![]() 的图象,再根据
的图象,再根据![]() 经过点
经过点![]() ,画出图象即可;
,画出图象即可;
(3)设直线![]() 的解析式为y=
的解析式为y=![]() x+a,将点
x+a,将点![]() 代入,求出a的值,令y=0得到点D的坐标,以及点B的坐标,得到BD的值,联立方程组得到点C的坐标,根据S△ABC= S△ABD+ S△DBC即可求出
代入,求出a的值,令y=0得到点D的坐标,以及点B的坐标,得到BD的值,联立方程组得到点C的坐标,根据S△ABC= S△ABD+ S△DBC即可求出![]() 的面积.
的面积.
解:(1)设直线![]() 的解析式为y=kx+b,将点
的解析式为y=kx+b,将点![]() 代入得:
代入得:
![]() ,解得:k=
,解得:k=![]() ,b=-3,
,b=-3,
∴直线![]() 的解析式为y=
的解析式为y=![]() x-3;
x-3;
(2)如下图所示,直线![]() 为所求;
为所求;

(3)设直线![]() 的解析式为y=
的解析式为y=![]() x+a,将点
x+a,将点![]() 代入得:a=2,
代入得:a=2,
∴y=![]() x+2,
x+2,
设直线![]() 与x轴交于点D,则当y=0时,
与x轴交于点D,则当y=0时,![]() x+2=0,解得x=
x+2=0,解得x=![]() ,
,
∴D(![]() ,0),
,0),
∵直线![]() ,当y=0时,
,当y=0时,![]() ,解得:x=
,解得:x=![]() ,
,
∴B(![]() ,0),
,0),
则BD=![]() -
-![]() =2,
=2,
由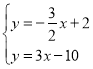 得:
得: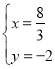 ,
,
∴C(![]() ,-2),
,-2),
过点C作CE⊥x轴于点E,则CE=2,
∴S△ABC= S△ABD+ S△DBC=![]() BDAO+
BDAO+![]() BDCE=
BDCE=![]() ×2×2+
×2×2+![]() ×2×2=4,
×2×2=4,
∴![]() 的面积为4.
的面积为4.

练习册系列答案
相关题目