Question

【题目】通过类比联想，引申拓展研究典型题目，可达到解一题知一类的目的.下面是一个案例，先阅读再解决后面的问题：

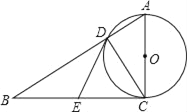
原题：如图1，点E，F分别在正方形ABCD的边BC，CD上，，连接EF，求证：EF=BE+DF.

解题由于AB=AD，我们可以延长CD到点G，使DG=BE，易得，可证.再证明，得EF=FG=DG+FD=BE+DF.

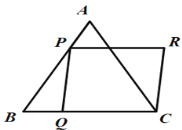
问题（1）：如图2，在四边形ABCD中，AB=AD，，E，F分别是边BC，CD上的点，且，求证：EF=BE+FD；

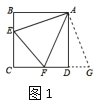
问题（2）：如图3，在四边形ABCD中，，，AB=AD=1，点E，F分别在四边形ABCD的边BC，CD上的点，且，求此时的周长

Answer 1

【答案】（1），见解析；（2）周长为.

【解析】

（1）在CD的延长线上截取DG=BE，连接AG，证出△ABE≌△ADG，根据全等三角形的性质得出BE=DG，再证明△AEF≌△AGF，得EF=FG，即可得出答案；
（2）连接AC，证明△ABC≌△ADC（SSS）．得∠DAC=∠BAC，同理由（1）得EF=BE+DF，可计算△CEF的周长．

证明：（1）在CD的延长线上截取DG=BE，连接AG，如图2，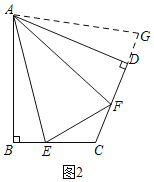

∵∠ADF=90°，∠ADF+∠ADG=180°，
∴∠ADG=90°，
∵∠B=90°，
∴∠B=∠ADG=90°，
∵BE=DG，AB=AD，
∴△ABE≌△ADG（SAS），
∴∠BAE=∠DAG，AG=AE，
∴∠EAG=∠EAD+∠DAG=∠EAD+∠ABE=∠BAD，
∵∠EAF=∠BAD，
∵∠EAG=∠EAG=（∠EAF+∠FAG），
∴∠EAF=∠FAG，
又∵AF=AF，AE=AG，
∴△AEF≌△AFG（SAS），
∴EF=FG=DF+DG=EB+DF；
（2）解：连接AC，如图3，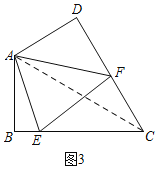

∵AB=AD，BC=CD，AC=AC，
∴△ABC≌△ADC（SSS）．
∴∠DAC=∠BAC，
∴∠BAC=∠BAD=60°，
∵∠B=90°，AB=1，
∴在Rt△ABC中，AC=2，BC===,
由（1）得EF=BE+DF，
∴△CEF的周长=CE+CF+EF=2BC=2．