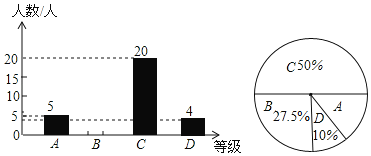
题目内容
【题目】在平面直角坐标系中,点![]() ,点
,点![]() .将
.将![]() 绕点
绕点![]() 顺时针旋转,得
顺时针旋转,得![]() ,点
,点![]() ,
,![]() 旋转后的对应点为
旋转后的对应点为![]() ,
,![]() .记旋转角为
.记旋转角为![]() .
.
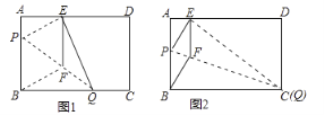
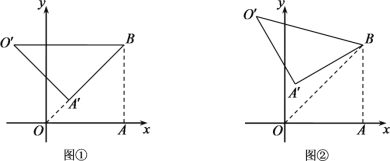
(1)如图①,当![]() 时,求点
时,求点![]() 的坐标;
的坐标;
(2)如图②,当![]() 时,求点
时,求点![]() 的坐标;
的坐标;
(3)连接![]() ,设线段
,设线段![]() 的中点为
的中点为![]() ,连接
,连接![]() ,求线段
,求线段![]() 的长的最小值(直接写出结果即可).
的长的最小值(直接写出结果即可).
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】
(1)过点![]() 作
作![]() ,垂足为
,垂足为![]() ,根据题意可得
,根据题意可得![]() ,
,![]() ,从而求出
,从而求出![]() ,
,![]() ,根据旋转的性质
,根据旋转的性质![]() ,点
,点![]() 在线段
在线段![]() 上,然后利用锐角三角函数即可求出结论;
上,然后利用锐角三角函数即可求出结论;
(2)连接![]() ,过点
,过点![]() 作
作![]() ,垂足为
,垂足为![]() ,根据旋转的性质
,根据旋转的性质![]() ,
,![]() ,然后利用锐角三角函数可得
,然后利用锐角三角函数可得![]() ,
,![]() ,求出OD,即可得出结论;
,求出OD,即可得出结论;
(3)连接![]() ,设线段
,设线段![]() 的中点为
的中点为![]() ,连接
,连接![]() ,取
,取![]() 的中点N,连接
的中点N,连接![]() 、MN,根据中位线的性质可得MN=
、MN,根据中位线的性质可得MN=![]() OB=
OB=![]() ,利用勾股定理求出
,利用勾股定理求出![]() ,然后根据三角形的三边关系即可得出结论.
,然后根据三角形的三边关系即可得出结论.
解:(1)如图,过点![]() 作
作![]() ,垂足为
,垂足为![]() .
.
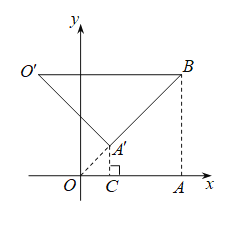
∵ 点![]() ,点
,点![]() ,
,
∴ ![]() ,
,![]() .
.
∴ ![]() ,
,![]() .
.
∵ ![]() 是
是![]() 绕点
绕点![]() 顺时针旋转得到的,
顺时针旋转得到的,![]() ,
,
∴ ![]() ,点
,点![]() 在线段
在线段![]() 上.
上.
∴ ![]() .
.
在![]() 中,
中,![]() ,
,![]() .
.
∴ 点![]() 的坐标为
的坐标为![]() .
.
(2)如图,连接![]() ,过点
,过点![]() 作
作![]() ,垂足为
,垂足为![]() .
.
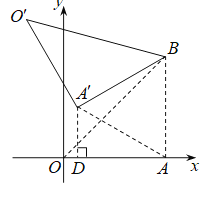
∵ ![]() ,
,![]() ,
,
∴ ![]() ,
,![]() .
.
∴ ![]() .
.
在![]() 中,
中,![]() ,
,![]() .
.
∴ ![]() .
.
∴ 点![]() 的坐标为
的坐标为![]() .
.
(3)连接![]() ,设线段
,设线段![]() 的中点为
的中点为![]() ,连接
,连接![]() ,取
,取![]() 的中点N,连接
的中点N,连接![]() 、MN
、MN
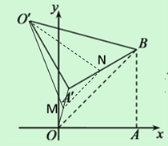
∴MN为△A′OB的中位线,![]()
∴MN=![]() OB=
OB=![]()
由勾股定理可得![]()
∴![]() ≥
≥![]() -MN=
-MN=![]() (当且仅当M 在线段O′N上时,取等号)
(当且仅当M 在线段O′N上时,取等号)
∴![]() 的最小值为
的最小值为![]() .
.

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目