��Ŀ����
����С������9�֣���
 �У�
�� ����
���� ��
�� ���ڵ�ֱ�����˶�����
���ڵ�ֱ�����˶����� ��
�� ����ʱ�뷽��
����ʱ�뷽����1����ͼ1������
 ���߶�
���߶� ���˶���
���˶��� ��
�� ��
�� ��
�����ʡ�ABD���DCE������?Ϊʲô?
�ڵ�
 �ǵ���������ʱ����
�ǵ���������ʱ���� �ij���
�ij�����2������ͼ2������
 ��
�� ���ӳ������˶���
���ӳ������˶��� �ķ����ӳ�����
�ķ����ӳ����� ���ӳ����ཻ�ڵ�
���ӳ����ཻ�ڵ� ���Ƿ���ڵ�
���Ƿ���ڵ� ��ʹ
��ʹ �ǵ��������Σ������ڣ�д�����е�
�ǵ��������Σ������ڣ�д�����е� ��λ�ã��������ڣ����Ҫ˵�����ɣ�
��λ�ã��������ڣ����Ҫ˵�����ɣ�����ͼ3������
 ��
�� �ķ����ӳ������˶����Ƿ���ڵ�
�ķ����ӳ������˶����Ƿ���ڵ� ��ʹ
��ʹ �ǵ��������Σ������ڣ�д�����е�
�ǵ��������Σ������ڣ�д�����е� ��λ�ã��������ڣ����Ҫ˵�����ɣ�
��λ�ã��������ڣ����Ҫ˵�����ɣ�

��֤���� ����������������������������������������1��
����������������������������������������1��
������:�� ����
����
���B=��C=45���� ��ADE=45��
���ADB+��EBC=��EBC+��DEC=135��
���ADB=��DEC �� 
�� �� �ǵ���������ʱ,�����������������
�ǵ���������ʱ,�����������������
��һ�������DE=AE
��DE=AE
���ADE=��DAE=45��
�� ��AED=90��, ��ʱ��EΪAC���е㣬��AE= AC=1.
AC=1.
�ڶ��������AD=AE��D��B�غϣ�
AE=2������������������������������������������������������������5��
��������� ��AD=AE
���AD=DE������ ��
��
�� ��ABD�ա�DCE,
��BD=CE,AB=DC,��BD=CE=
�� ����
���� ��
��
�� BC= , DC=
, DC= ��
��
�� ��
�� ="2" ,��ã�
="2" ,��ã� =
= ��2 ��
��2 ��
�� AE=" 4" ��2 ����������������������������������������������6��
����������������������������������������������6��
����������AE��ֵ��1��2��4 ��2
(2)�ٴ��ڡ�
��D��BC���ӳ����ϣ���CD=CAʱ�� �ǵ���������.֤�����ߡ�ADE=45��=��ACB=��DCE��,
�ǵ���������.֤�����ߡ�ADE=45��=��ACB=��DCE��,
�� ��ADC+��EDC=��EDC+��DEC=135��,
�� ��ADC=��DEC,��CD="CA" ��
�� ��CAD=��CDA ,
�� ��CAD=��CED ,
��DA=DE��,
��  �ǵ���������.�ڲ�����.
�ǵ���������.�ڲ�����.
��Ϊ��ACD=45�㣾��E , ��ADE=45��
���ADE�١�E�� �������ǵ��������Ρ�����:
�������ǵ��������Ρ�����:
��
 ����������������������������������������1��
����������������������������������������1��������:��
 ����
����
���B=��C=45���� ��ADE=45��
|
|

�� ��
 �ǵ���������ʱ,�����������������
�ǵ���������ʱ,�������������������һ�������DE=AE
��DE=AE
���ADE=��DAE=45��
|
 AC=1.
AC=1.�ڶ��������AD=AE��D��B�غϣ�
AE=2������������������������������������������������������������5��
��������� ��AD=AE
���AD=DE������
 ��
���� ��ABD�ա�DCE,
��BD=CE,AB=DC,��BD=CE=

��
 ����
���� ��
�� �� BC=
 , DC=
, DC= ��
��
��
 ��
�� ="2" ,��ã�
="2" ,��ã� =
= ��2 ��
��2 ���� AE=" 4" ��2
 ����������������������������������������������6��
����������������������������������������������6������������AE��ֵ��1��2��4 ��2

(2)�ٴ��ڡ�
|
 �ǵ���������.֤�����ߡ�ADE=45��=��ACB=��DCE��,
�ǵ���������.֤�����ߡ�ADE=45��=��ACB=��DCE��, �� ��ADC+��EDC=��EDC+��DEC=135��,
�� ��ADC=��DEC,��CD="CA" ��
�� ��CAD=��CDA ,
�� ��CAD=��CED ,
��DA=DE��,
|
 �ǵ���������.�ڲ�����.
�ǵ���������.�ڲ�����.��Ϊ��ACD=45�㣾��E , ��ADE=45��
|
 �������ǵ��������Ρ�����:
�������ǵ��������Ρ�����:��

��ϰ��ϵ�д�
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
�����Ŀ
 ��
��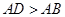 ���У���ֽƬ�۵�һ�Σ�ʹ��
���У���ֽƬ�۵�һ�Σ�ʹ��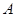 ��
�� �غϣ���չ�����ۺ�
�غϣ���չ�����ۺ� ��
�� ����
���� ����
���� ����
����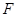 ���ֱ�����
���ֱ����� ��
�� ��
��
 ������
������ ��
�� ��
�� ����֤��
����֤��
 ��
�� �����Ϊ
�����Ϊ ����
����
 Ϊ�뾶��Բ���ڲ��ĸ���.
Ϊ�뾶��Բ���ڲ��ĸ���. ͼ���ϣ�����B��BD��x�ᣬ����ΪD����B�������Ϊ��3��
ͼ���ϣ�����B��BD��x�ᣬ����ΪD����B�������Ϊ��3��