Ő‚ńŅńŕ»›
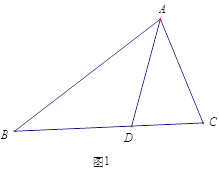
°ĺŐ‚ńŅ°Ņ»ÁÕľ£¨°ųABC «Ķ»ĪŖ»żĹ«–ő£¨Ķ„D°ĘE∑÷Īū «…šŌŖAB°Ę…šŌŖCB…ŌĶń∂ĮĶ„£¨Ķ„Dī”Ķ„A≥Ų∑Ę—ō…šŌŖAB“∆∂Į£¨Ķ„Eī”Ķ„B≥Ų∑Ę—ōBG“∆∂Į£¨Ķ„D°ĘĶ„EÕ¨ Ī≥Ų∑Ę≤Ę«“‘ň∂ĮňŔ∂»ŌŗÕ¨£ģѨŔCD°ĘDE£ģ
£®1£©»ÁÕľĘŔ£¨ĶĪĶ„D“∆∂ĮĶĹŌŖ∂őABĶń÷–Ķ„ Ī£¨«ů÷§£ļDE=DC£ģ
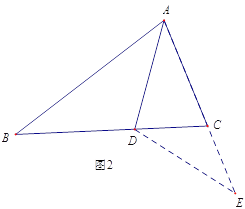
£®2£©»ÁÕľĘŕ£¨ĶĪĶ„D‘ŕŌŖ∂őAB…Ō“∆∂ĮĶę≤Ľ «÷–Ķ„ Ī£¨ ‘ŐĹňųDE”ŽDC÷ģľšĶń żŃŅĻōŌĶ£¨≤ĘňĶ√ųņŪ”…£ģ
£®3£©»ÁÕľĘŘ£¨ĶĪĶ„D“∆∂ĮĶĹŌŖ∂őABĶń—”≥§ŌŖ…Ō£¨≤Ę«“ED°ÕDC Ī£¨«ů°ŌDEC∂» ż£ģ
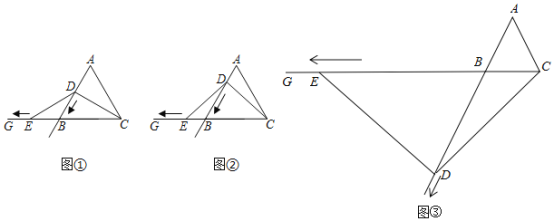
°ĺīūįł°Ņ£®1£©ľŻŌÍĹ‚£Ľ
£®2£©DE=DC£¨ņŪ”…ľŻŌÍĹ‚£Ľ
£®3£©°ŌDEC=45°„
°ĺĹ‚őŲ°Ņ
£®1£©”…Ő‚“‚Ņ…÷™![]() £¨ňý“‘
£¨ňý“‘![]() £¨”…Ķ»ĪŖ»żĹ«–őľį÷–Ķ„Ņ…÷™
£¨”…Ķ»ĪŖ»żĹ«–őľį÷–Ķ„Ņ…÷™![]() £¨∂Ý
£¨∂Ý![]() £¨ňý“‘Ņ…÷§
£¨ňý“‘Ņ…÷§![]() £¨ĹÝ“Ľ≤ĹŅ…÷§
£¨ĹÝ“Ľ≤ĹŅ…÷§![]()
£®2£©≤¬≤‚![]() £¨—į’“ŐűľĢ÷§√ųľīŅ….◊Ó≥£”√Ķń «÷§√ųŃĹłŲ»żĹ«–ő»ęĶ»£¨ĶęÕľ÷–łÝ≥ŲĶń»żĹ«–ő÷–≤Ęőī≥ŲŌ÷»ęĶ»»żĹ«–ő£¨ňý“‘ŐŪľ”ł®÷ķŌŖ£ļ‘ŕ…šŌŖAB…ŌĹō»°
£¨—į’“ŐűľĢ÷§√ųľīŅ….◊Ó≥£”√Ķń «÷§√ųŃĹłŲ»żĹ«–ő»ęĶ»£¨ĶęÕľ÷–łÝ≥ŲĶń»żĹ«–ő÷–≤Ęőī≥ŲŌ÷»ęĶ»»żĹ«–ő£¨ňý“‘ŐŪľ”ł®÷ķŌŖ£ļ‘ŕ…šŌŖAB…ŌĹō»°![]() £¨’‚—ý÷Ľ“™÷§√ų
£¨’‚—ý÷Ľ“™÷§√ų![]() ľīŅ….ņŻ”√Ķ»ĪŖ»żĹ«–őĶń–‘÷ ľį
ľīŅ….ņŻ”√Ķ»ĪŖ»żĹ«–őĶń–‘÷ ľį![]() Ņ…÷™
Ņ…÷™![]() ő™Ķ»ĪŖ»żĹ«–ő£¨’‚—ýÕ®ĻżŃĹłŲĶ»ĪŖ»żĹ«–őľīŅ…÷§√ų
ő™Ķ»ĪŖ»żĹ«–ő£¨’‚—ýÕ®ĻżŃĹłŲĶ»ĪŖ»żĹ«–őľīŅ…÷§√ų![]() .
.
£®3£©įī’’Ķŕ£®2£©ő Ķńňľ¬∑£¨◊ų≥Ųņŗň∆Ķńł®÷ķŌŖ£ļ‘ŕ…šŌŖCB…ŌĹō»°![]() £¨”√Õ¨—ýĶń∑Ĺ∑®÷§√ų
£¨”√Õ¨—ýĶń∑Ĺ∑®÷§√ų![]() £¨”÷“Úő™ED°ÕDC£¨ňý“‘
£¨”÷“Úő™ED°ÕDC£¨ňý“‘![]() ő™Ķ»—Ł÷ģľš»żĹ«–ő£¨‘Ú°ŌDEC∂» żŅ…«ů.
ő™Ķ»—Ł÷ģľš»żĹ«–ő£¨‘Ú°ŌDEC∂» żŅ…«ů.
”…Ő‚“‚Ņ…÷™![]()
°ŖDő™ABĶń÷–Ķ„
![]()
![]()
![]()
°Ŗ![]() ő™Ķ»ĪŖ»żĹ«–ő£¨
ő™Ķ»ĪŖ»żĹ«–ő£¨![]()
![]()
![]()
![]()
![]()
![]()
£®2£©![]()
ņŪ”…»ÁŌ¬£ļ
‘ŕ…šŌŖAB…ŌĹō»°![]() £¨Ń¨Ĺ”EF
£¨Ń¨Ĺ”EF

°Ŗ![]() ő™Ķ»ĪŖ»żĹ«–ő
ő™Ķ»ĪŖ»żĹ«–ő
![]()
![]()
°ŗ![]() ő™Ķ»ĪŖ»żĹ«–ő
ő™Ķ»ĪŖ»żĹ«–ő
![]()
”…Ő‚“‚÷™![]()
![]()
![]()
ľī![]()
![]()
![]()
‘ŕ![]() ļÕ
ļÕ![]() ÷–£¨
÷–£¨
![]()
![]()
£®3£©»ÁÕľ£¨‘ŕ…šŌŖCB…ŌĹō»°![]() £¨Ń¨Ĺ”DF
£¨Ń¨Ĺ”DF

°Ŗ![]() ő™Ķ»ĪŖ»żĹ«–ő
ő™Ķ»ĪŖ»żĹ«–ő
![]()
![]()
°ŗ![]() ő™Ķ»ĪŖ»żĹ«–ő
ő™Ķ»ĪŖ»żĹ«–ő
![]()
![]()
”…Ő‚“‚÷™![]()
![]()
![]()
ľī![]()
![]()
![]()
‘ŕ![]() ļÕ
ļÕ![]() ÷–£¨
÷–£¨
![]()
![]()
°ŖED°ÕDC
°ŗ![]() ő™Ķ»—Ł÷ĪĹ«»żĹ«–ő
ő™Ķ»—Ł÷ĪĹ«»żĹ«–ő
![]()