��Ŀ����
����Ŀ����ͼ���ڵȱ�![]() �У�
��![]() ������
������![]() �ӵ�
�ӵ�![]() ������
������![]() ���ٶ���
���ٶ���![]() �����˶�(��
�����˶�(��![]() ��
��![]() ���غ�)������
���غ�)������![]() ͬʱ�ӵ�
ͬʱ�ӵ�![]() ������ͬ�����ٶ���
������ͬ�����ٶ���![]() ���ӳ��߷��������˶�������
���ӳ��߷��������˶�������![]() �����
�����![]() ʱ����
ʱ����![]() ��
��![]() ͬʱֹͣ�˶�(
ͬʱֹͣ�˶�(![]() ����
����![]() �غ�)�����˶�ʱ��Ϊ��
�غ�)�����˶�ʱ��Ϊ��![]() (
(![]() )����
)����![]() ��
��![]() ��
��![]() ������
������![]() ��
�� ![]() ��
��![]() .
.

��1��![]()
![]() ��
��![]()
![]() �����ú�
�����ú� ![]() �Ĵ���ʽ��ʾ��
�Ĵ���ʽ��ʾ��
��2����![]() Ϊ��ֵʱ��
Ϊ��ֵʱ��![]() Ϊֱ�������Σ�
Ϊֱ�������Σ�
��3����![]() ��
��![]() ���ӳ��ߵķ���ƽ�Ƶ�
���ӳ��ߵķ���ƽ�Ƶ� ![]() ����
����![]() ���Ƿ����ijһʱ��
���Ƿ����ijһʱ��![]() ��ʹ��
��ʹ��![]() ��
��![]() ��ƽ�����ϣ������ڣ����
��ƽ�����ϣ������ڣ����![]() ��ֵ���������ڣ���˵�����ɣ�
��ֵ���������ڣ���˵�����ɣ�
��4�����˶��������߶�![]() �ij��Ƿ����仯��������䣬����߶�
�ij��Ƿ����仯��������䣬����߶�![]() �ij���
�ij���
���𰸡���1��![]() ��
��![]() ����2��
����2��![]() ����3�����ڣ�
����3�����ڣ�![]() �����ɼ���������4��
�����ɼ���������4��![]()
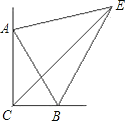
��������
��1��P��Q�ٶȶ�Ϊ1cm/s�����ٶȳ�ʱ��ɵõ��˶�·�̾�Ϊtcm��PC�ij���Ϊ�ȱ������α߳���ȥt��QC�ij���Ϊ�߳�����t�����ɵõ��𰸣�
��2������CPQΪֱ��������ʱ����Q=30�㣬����ֱ����������30�����Ե�ֱ�DZ���б�ߵ�һ�뽨��������⣻
��3������![]() ��
��![]() ��
��![]() ���ɽ�ƽ���ߺ�ƽ�У���
���ɽ�ƽ���ߺ�ƽ�У���![]() ������ֱ����������30�����Ե�ֱ�DZ���б�ߵ�һ�룬�ɵ�
������ֱ����������30�����Ե�ֱ�DZ���б�ߵ�һ�룬�ɵ�![]() ��Ȼ��������t�ķ�����⣻
��Ȼ��������t�ķ�����⣻
��4������![]() ��
��![]() ����ֱ��
����ֱ��![]() ���ӳ����ڵ�
���ӳ����ڵ�![]() ��������AAS֤��
��������AAS֤��![]() ��
��![]() ���õ�
���õ�![]() ��
��![]() ��Ȼ����
��Ȼ����![]() ��
��![]() ���Ƴ�
���Ƴ�![]() ��������߶ε��������ɵ�
��������߶ε��������ɵ�![]() �����ɵó�EDʼ��Ϊ�ȱ������α߳���һ��.
�����ɵó�EDʼ��Ϊ�ȱ������α߳���һ��.
�⣺��1����P��Q�ٶȶ�Ϊ1cm/s��
��BQ=AP=tcm
��PC=AC-AP=![]() ��QC=BC+BQ=
��QC=BC+BQ=![]()
�ʴ�Ϊ��![]() ��
��![]() ��
��
��2��������CPQΪֱ��������ʱ����Q=30��
��![]() ����
����![]() �����
�����![]()
���Ե�![]() =2��
=2��![]() Ϊֱ�������Σ�
Ϊֱ�������Σ�
��3������.
���ɣ���ͼ������![]() ��
��![]() ��
��![]()
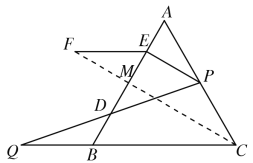
���ڵȱ�������ABC�У�CF�ǡ�ACB�Ľ�ƽ���ߣ�
��![]() ��
��![]()
��![]()
��![]()
��![]()
��Rt��AEP�У���APE=30�㣬
��AE=![]() AP=
AP=![]()
��EM=AM-AE
��![]()
��![]()
���![]()
���Ե�![]() ʱ����
ʱ����![]() ��
��![]() ��ƽ������.
��ƽ������.
��4������![]() ��
��![]() �˶�ʱ���߶�
�˶�ʱ���߶�![]() �ij��Ȳ���ı䣬�������£�
�ij��Ȳ���ı䣬�������£�
����![]() ��
��![]() ����ֱ��
����ֱ��![]() ���ӳ����ڵ�
���ӳ����ڵ�![]()

����![]() ��
��![]()
��![]()
����![]() ��
��![]() �ٶ���ͬ
�ٶ���ͬ
��![]()
��![]() �ǵȱ������Σ�
�ǵȱ������Σ�
��![]()
��![]() ��
��![]() ��
��
��![]() ��
��![]() ��
��![]()
��![]() ��
��![]() ��
��![]() ��
��
��![]() ��
��![]()
��![]() ��
��![]() ��
��
�ߡ�PDE=��QDH����PED=��QHD��PE=QH
��![]() ��
��![]() ��
��![]() ��
��
��![]() ����
����![]()
��![]()
��![]()
�����ȱ�![]() �ı߳�Ϊ6
�ı߳�Ϊ6
��![]()
�������˶��������߶�![]() �ij����ᷢ���仯��
�ij����ᷢ���仯��![]() ��
��