��Ŀ����
����Ŀ������������![]() �֣�
�֣�
��![]() �������⡿��ͼ
�������⡿��ͼ![]() ����
����![]() Ϊ�߶�
Ϊ�߶�![]() ��һ���㣬��
��һ���㣬��![]() ��
�� ![]() ������
������![]() λ��__________ʱ�߶�
λ��__________ʱ�߶�![]() �ij�ȡ�����ֵ�������ֵΪ__________���ú�
�ij�ȡ�����ֵ�������ֵΪ__________���ú�![]() ��
��![]() ��ʽ�ӱ�ʾ����
��ʽ�ӱ�ʾ����
��![]() ����Ӧ�á���
����Ӧ�á���![]() Ϊ�߶�
Ϊ�߶�![]() ����һ���㣬��
����һ���㣬��![]() ��
�� ![]() ����ͼ
����ͼ![]() ��ʾ���ֱ���
��ʾ���ֱ���![]() ��
��![]() Ϊ�ߣ�
Ϊ�ߣ�
���ȱ�������![]() �͵ȱ�������
�͵ȱ�������![]() ������
������![]() ��
��![]() ��
��
�����ҳ�ͼ����![]() ��ȵ��߶Σ���˵�����ɣ�
��ȵ��߶Σ���˵�����ɣ�
��ֱ��д���߶�![]() �������ֵ��
�������ֵ��
��![]() ������չ����ͼ
������չ����ͼ![]() ����ƽ��ֱ������ϵ�У���
����ƽ��ֱ������ϵ�У���![]() ������Ϊ
������Ϊ![]() ����
����![]() ������Ϊ
������Ϊ![]() ����
����![]() Ϊ�߶�
Ϊ�߶�
![]() ��һ���㣬��
��һ���㣬��![]() ��
�� ![]() ��
�� ![]() ����ֱ��д���߶�
����ֱ��д���߶�![]() �������ֵ����ʱ��
�������ֵ����ʱ��![]() �����꣮
�����꣮




���𰸡���![]() ��
��![]() �ӳ����ϣ�
�ӳ����ϣ� ![]() ����
����![]() ����
����![]() ����
����![]() ��
��![]() ��
��![]() ��
�� ![]()
����������![]() �������㲻����ʱ������������֮�ʹ��ڵ����ߣ���
�������㲻����ʱ������������֮�ʹ��ڵ����ߣ���![]() ��
��
��![]() ��
��![]() �ӳ�����ʱ��
�ӳ�����ʱ�� ![]() ��
��
��![]() ���߶�
���߶�![]() ��ʱ��
��ʱ�� ![]() ��
��
�ʵ�![]() ��
��![]() �ӳ�����ʱ��
�ӳ�����ʱ�� ![]() ȡ�����ֵ����Ϊ
ȡ�����ֵ����Ϊ![]() ��
��
��![]() �����������
�����������![]() ��
�� ![]() �����õȱ�������ÿ���Ƕ���
�����õȱ�������ÿ���Ƕ���![]() �ͽǵĹ�ϵ��
�ͽǵĹ�ϵ��![]() ��
��
�����ݱ߽DZ߶���֤��![]() ��
��![]() ��
��
�Ӷ��Ƴ�![]() ��
��
����Ϊ![]() �������߶�
�������߶�![]() �����ֵ��
�����ֵ��![]() �����ֵ��
�����ֵ��
��������������֮�ʹ��ڵ����ߣ�����![]() ���ʱ��
���ʱ��![]() ��
��![]() ��
��![]() ���㹲�ߣ�
���㹲�ߣ�
�õ�![]() �����ֵΪ
�����ֵΪ![]() ��
��
��![]() �����ֵΪ
�����ֵΪ![]() ��
��
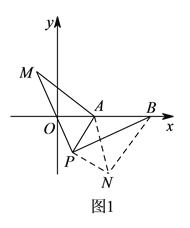
��![]() ����ͼ1���Ե�
����ͼ1���Ե�![]() ΪԲ�ģ�
ΪԲ�ģ� ![]() Ϊ�뾶���������Ե�
Ϊ�뾶���������Ե�![]() ΪԲ�ģ�
ΪԲ�ģ�
![]() Ϊ�뾶���Ļ��ڵ�
Ϊ�뾶���Ļ��ڵ�![]() ������
������![]() ��
��![]() ��
��![]() ����
����![]() ��
��
��![]() ��
��![]() ��
�У�
 ��
��
����![]() ��
��![]() ��
��
����![]() ������Ϊ
������Ϊ![]() ��
��
����![]() ����
����![]() ��
��
�ɣ�![]() ����֪������
����֪������![]() ��
��![]() ���ӳ�����ʱ��
���ӳ�����ʱ�� ![]() ȡ�����ֵ��
ȡ�����ֵ��
����Ϊ![]() �����Դ�ʱ
�����Դ�ʱ![]() ȡ�����ֵ��
ȡ�����ֵ��
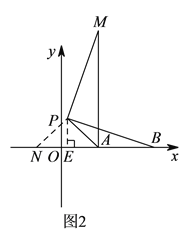
��ͼ2����![]() ��
��![]() ���ӳ�����ʱ������
���ӳ�����ʱ������![]() ��
��![]() ���ڵ�
���ڵ�![]() ��
��
��![]() �У��ɹ��ɶ�����
�У��ɹ��ɶ�����
![]() ��
��
����![]() ��
��
��Ϊ![]() ��
�� ![]() ������
������![]() �ǵ���ֱ�������Σ�
�ǵ���ֱ�������Σ�
����Ϊ![]() ������
������![]() ��
��
������![]() ��
��
����![]() ��
��
���Ե�![]() ����Ϊ
����Ϊ![]() ��
��