Question

勾股定理是几何中的一个重要定理．在我国古算书《周髀算经》中就有“若勾三，股四，则弦五”的记载．如图1是由边长相等的小正方形和直角三角形构成的，可以用其面积关系验证勾股定理．图2是由图1放入矩形内得到的，∠BAC=90°，AB=3，AC=4，点D，E，F，G，H，I都在矩形KLMJ的边上，则矩形KLMJ的面积为（　　）

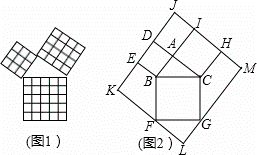
　　A．90　　B．100　　C．110　　D．121

Answer 1

考点：

勾股定理的证明。

专题：

常规题型。

分析：

延长AB交KF于点O，延长AC交GM于点P，可得四边形AOLP是正方形，然后求出正方形的边长，再求出矩形KLMJ的长与宽，然后根据矩形的面积公式列式计算即可得解．

解答：

解：如图，延长AB交KF于点O，延长AC交GM于点P，

所以，四边形AOLP是正方形，

边长AO=AB+AC=3+4=7，

所以，KL=3+7=10，LM=4+7=11，

因此，矩形KLMJ的面积为10×11=110．

故选C．

点评：

本题考查了勾股定理的证明，作出辅助线构造出正方形是解题的关键．