题目内容
 如图,正△ABC的边长为3,绕其中心O将△ABC旋转180°得到△DEF,则△ABC和△DEF重叠部分的面积为
如图,正△ABC的边长为3,绕其中心O将△ABC旋转180°得到△DEF,则△ABC和△DEF重叠部分的面积为
- A.

- B.

- C.

- D.

A
分析:根据等边三角形的特殊性,重叠部分为正六边形,四周空白部分的小三角形是等边三角形,从而得出重叠部分的面积是△ABC与三个小等边三角形的面积之差.
解答:根据旋转的意义,图中空白部分的小三角形也是等边三角形,且边长为1,面积是△ABC的 .
.
仔细观察图形,重叠部分的面积是△ABC与三个小等边三角形的面积之差,
△ABC的面积是 ,一个小等边三角形的面积是
,一个小等边三角形的面积是 ,所以重叠部分的面积是
,所以重叠部分的面积是 .
.
故选A.
点评:本题考查了图形的旋转变化,三角形面积的求法,难度不大,但容易错.
分析:根据等边三角形的特殊性,重叠部分为正六边形,四周空白部分的小三角形是等边三角形,从而得出重叠部分的面积是△ABC与三个小等边三角形的面积之差.
解答:根据旋转的意义,图中空白部分的小三角形也是等边三角形,且边长为1,面积是△ABC的
 .
.仔细观察图形,重叠部分的面积是△ABC与三个小等边三角形的面积之差,
△ABC的面积是
 ,一个小等边三角形的面积是
,一个小等边三角形的面积是 ,所以重叠部分的面积是
,所以重叠部分的面积是 .
.故选A.
点评:本题考查了图形的旋转变化,三角形面积的求法,难度不大,但容易错.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目
 如图,正△ABC的边长为3,绕其中心O将△ABC旋转180°得到△DEF,则△ABC和△DEF重叠部分的面积为( )
如图,正△ABC的边长为3,绕其中心O将△ABC旋转180°得到△DEF,则△ABC和△DEF重叠部分的面积为( )A、
| ||||
B、
| ||||
C、
| ||||
D、6
|
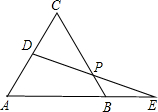 交BC于点P.
交BC于点P.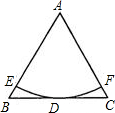 如图,正△ABC的边长AB=2,以A为圆心的圆切BC于点D,交AB于点E,交AC于点F,则弧EF的长=
如图,正△ABC的边长AB=2,以A为圆心的圆切BC于点D,交AB于点E,交AC于点F,则弧EF的长=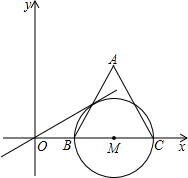 点,以BC为直径的⊙M交AB于E.
点,以BC为直径的⊙M交AB于E. (2012•内江)如图,正△ABC的边长为3cm,动点P从点A出发,以每秒1cm的速度,沿A→B→C的方向运动,到达点C时停止,设运动时间为x(秒),y=PC2,则y关于x的函数的图象大致为( )
(2012•内江)如图,正△ABC的边长为3cm,动点P从点A出发,以每秒1cm的速度,沿A→B→C的方向运动,到达点C时停止,设运动时间为x(秒),y=PC2,则y关于x的函数的图象大致为( )